ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

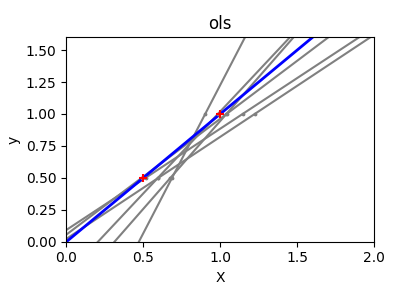
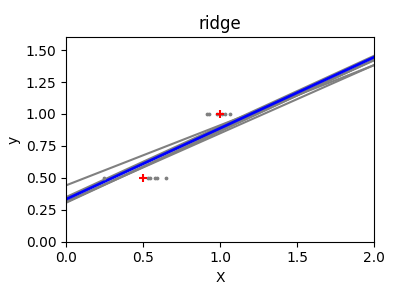
الانحدار الخطي العادي وانحدار ريدج والتباين#

بسبب قلة النقاط في كل بُعد والخط المستقيم الذي يستخدمه الانحدار الخطي لمتابعة هذه النقاط بأفضل ما يمكن، فإن الضوضاء على الملاحظات ستسبب تباينًا كبيرًا كما هو موضح في الرسم البياني الأول. يمكن أن يختلف ميل كل خط بشكل كبير لكل توقع بسبب الضوضاء في الملاحظات.

انحدار ريدج هو في الأساس تقليل نسخة مُعاقبة من دالة المربعات الصغرى. هذه العقوبة "تقلص" قيمة معاملات الانحدار. على الرغم من قلة نقاط البيانات في كل بُعد، فإن ميل التوقع أكثر استقرارًا، والتباين في الخط نفسه يقل بشكل كبير، مقارنة بالانحدار الخطي القياسي.

# المؤلفون: مطوري سكايلرن
# معرف الترخيص: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn import linear_model

X_train = np.c_[0.5, 1].T
y_train = [0.5, 1]
X_test = np.c_[0, 2].T

np.random.seed(0)

classifiers = dict(
    ols=linear_model.LinearRegression(), ridge=linear_model.Ridge(alpha=0.1)
)

for name, clf in classifiers.items():
    fig, ax = plt.subplots(figsize=(4, 3))

    for _ in range(6):
        this_X = 0.1 * np.random.normal(size=(2, 1)) + X_train
        clf.fit(this_X, y_train)

        ax.plot(X_test, clf.predict(X_test), color="gray")
        ax.scatter(this_X, y_train, s=3, c="gray", marker="o", zorder=10)

    clf.fit(X_train, y_train)
    ax.plot(X_test, clf.predict(X_test), linewidth=2, color="blue")
    ax.scatter(X_train, y_train, s=30, c="red", marker="+", zorder=10)

    ax.set_title(name)
    ax.set_xlim(0, 2)
    ax.set_ylim((0, 1.6))
    ax.set_xlabel("X")
    ax.set_ylabel("y")

    fig.tight_layout()

plt.show()