دعم الميزات التصنيفية في التدرج التعزيزي

في هذا المثال، سنقارن أوقات التدريب وأداء التنبؤ لـ HistGradientBoostingRegressor مع استراتيجيات الترميز المختلفة للميزات التصنيفية. على وجه الخصوص، سنقيم:

• إسقاط الميزات التصنيفية

• استخدام OneHotEncoder

• استخدام OrdinalEncoder واعتبار الفئات كميات متساوية ومتباعدة

• استخدام OrdinalEncoder والاعتماد على الدعم الأصلي للفئات لمقدر HistGradientBoostingRegressor.

سنعمل مع مجموعة بيانات Ames Iowa Housing التي تتكون من ميزات عددية وتصنيفية، حيث تكون أسعار مبيعات المنازل هي الهدف.

راجع الميزات في أشجار التعزيز المتدرج للهيستوغرام لمثال يبرز بعض الميزات الأخرى لـ HistGradientBoostingRegressor.

# المؤلفون: مطوري scikit-learn
# معرف SPDX-License: BSD-3-Clause

تحميل مجموعة بيانات Ames Housing

أولاً، نقوم بتحميل بيانات Ames Housing كإطار بيانات pandas. الميزات إما تصنيفية أو عددية:

from sklearn.datasets import fetch_openml

X, y = fetch_openml(data_id=42165, as_frame=True, return_X_y=True)

# حدد فقط مجموعة فرعية من ميزات X لجعل المثال أسرع في التشغيل
categorical_columns_subset = [
    "BldgType",
    "GarageFinish",
    "LotConfig",
    "Functional",
    "MasVnrType",
    "HouseStyle",
    "FireplaceQu",
    "ExterCond",
    "ExterQual",
    "PoolQC",
]

numerical_columns_subset = [
    "3SsnPorch",
    "Fireplaces",
    "BsmtHalfBath",
    "HalfBath",
    "GarageCars",
    "TotRmsAbvGrd",
    "BsmtFinSF1",
    "BsmtFinSF2",
    "GrLivArea",
    "ScreenPorch",
]

X = X[categorical_columns_subset + numerical_columns_subset]
X[categorical_columns_subset] = X[categorical_columns_subset].astype("category")

categorical_columns = X.select_dtypes(include="category").columns
n_categorical_features = len(categorical_columns)
n_numerical_features = X.select_dtypes(include="number").shape[1]

print(f"Number of samples: {X.shape[0]}")
print(f"Number of features: {X.shape[1]}")
print(f"Number of categorical features: {n_categorical_features}")
print(f"Number of numerical features: {n_numerical_features}")

Number of samples: 1460
Number of features: 20
Number of categorical features: 10
Number of numerical features: 10

مقدر التدرج التعزيزي مع إسقاط الميزات التصنيفية

كخط أساس، نقوم بإنشاء مقدر يتم فيه إسقاط الميزات التصنيفية:

from sklearn.compose import make_column_selector, make_column_transformer
from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.pipeline import make_pipeline

dropper = make_column_transformer(
    ("drop", make_column_selector(dtype_include="category")), remainder="passthrough"
)
hist_dropped = make_pipeline(dropper, HistGradientBoostingRegressor(random_state=42))

مقدر التدرج التعزيزي مع الترميز أحادي الساخن

بعد ذلك، نقوم بإنشاء خط أنابيب سيقوم بترميز الميزات التصنيفية باستخدام الترميز أحادي الساخن والسماح لبقية البيانات العددية بالمرور:

from sklearn.preprocessing import OneHotEncoder

one_hot_encoder = make_column_transformer(
    (
        OneHotEncoder(sparse_output=False, handle_unknown="ignore"),
        make_column_selector(dtype_include="category"),
    ),
    remainder="passthrough",
)

hist_one_hot = make_pipeline(
    one_hot_encoder, HistGradientBoostingRegressor(random_state=42)
)

مقدر التدرج التعزيزي مع الترميز الترتيبي

بعد ذلك، نقوم بإنشاء خط أنابيب سيعامل الميزات التصنيفية كما لو كانت كميات مرتبة، أي سيتم ترميز الفئات على أنها 0، 1، 2، إلخ، ويعامل على أنه ميزات مستمرة.

import numpy as np
import numpy as np

from sklearn.preprocessing import OrdinalEncoder

ordinal_encoder = make_column_transformer(
    (
        OrdinalEncoder(handle_unknown="use_encoded_value", unknown_value=np.nan),
        make_column_selector(dtype_include="category"),
    ),
    remainder="passthrough",
    # استخدام أسماء الميزات القصيرة لجعل من السهل تحديد المتغيرات التصنيفية في
    # HistGradientBoostingRegressor في الخطوة التالية
    # من خط الأنابيب.
    verbose_feature_names_out=False,
)

hist_ordinal = make_pipeline(
    ordinal_encoder, HistGradientBoostingRegressor(random_state=42)
)

مقدر التدرج التعزيزي مع الدعم التصنيفي الأصلي

نقوم الآن بإنشاء مقدر HistGradientBoostingRegressor الذي سيتعامل مع الميزات التصنيفية بشكل أصلي. لن يعتبر هذا المقدر الميزات التصنيفية كميات مرتبة. نحدد categorical_features="from_dtype" بحيث تعتبر الميزات ذات النوع التصنيفي ميزات تصنيفية.

الاختلاف الرئيسي بين هذا المقدر والمقدر السابق هو أنه في هذا المقدر، نسمح لـ HistGradientBoostingRegressor بالكشف عن الميزات التصنيفية من أنواع أعمدة DataFrame.

hist_native = HistGradientBoostingRegressor(
    random_state=42, categorical_features="from_dtype"
)

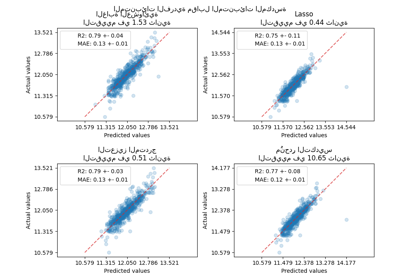
مقارنة النماذج

أخيرًا، نقوم بتقييم النماذج باستخدام التحقق المتقاطع. هنا نقارن أداء النماذج من حيث mean_absolute_percentage_error وأوقات التجهيز.

import matplotlib.pyplot as plt

from sklearn.model_selection import cross_validate

scoring = "neg_mean_absolute_percentage_error"
n_cv_folds = 3

dropped_result = cross_validate(hist_dropped, X, y, cv=n_cv_folds, scoring=scoring)
one_hot_result = cross_validate(hist_one_hot, X, y, cv=n_cv_folds, scoring=scoring)
ordinal_result = cross_validate(hist_ordinal, X, y, cv=n_cv_folds, scoring=scoring)
native_result = cross_validate(hist_native, X, y, cv=n_cv_folds, scoring=scoring)


def plot_results(figure_title):
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 8))

    plot_info = [
        ("fit_time", "Fit times (s)", ax1, None),
        ("test_score", "Mean Absolute Percentage Error", ax2, None),
    ]

    x, width = np.arange(4), 0.9
    for key, title, ax, y_limit in plot_info:
        items = [
            dropped_result[key],
            one_hot_result[key],
            ordinal_result[key],
            native_result[key],
        ]

        mape_cv_mean = [np.mean(np.abs(item)) for item in items]
        mape_cv_std = [np.std(item) for item in items]

        ax.bar(
            x=x,
            height=mape_cv_mean,
            width=width,
            yerr=mape_cv_std,
            color=["C0", "C1", "C2", "C3"],
        )
        ax.set(
            xlabel="Model",
            title=title,
            xticks=x,
            xticklabels=["Dropped", "One Hot", "Ordinal", "Native"],
            ylim=y_limit,
        )
    fig.suptitle(figure_title)


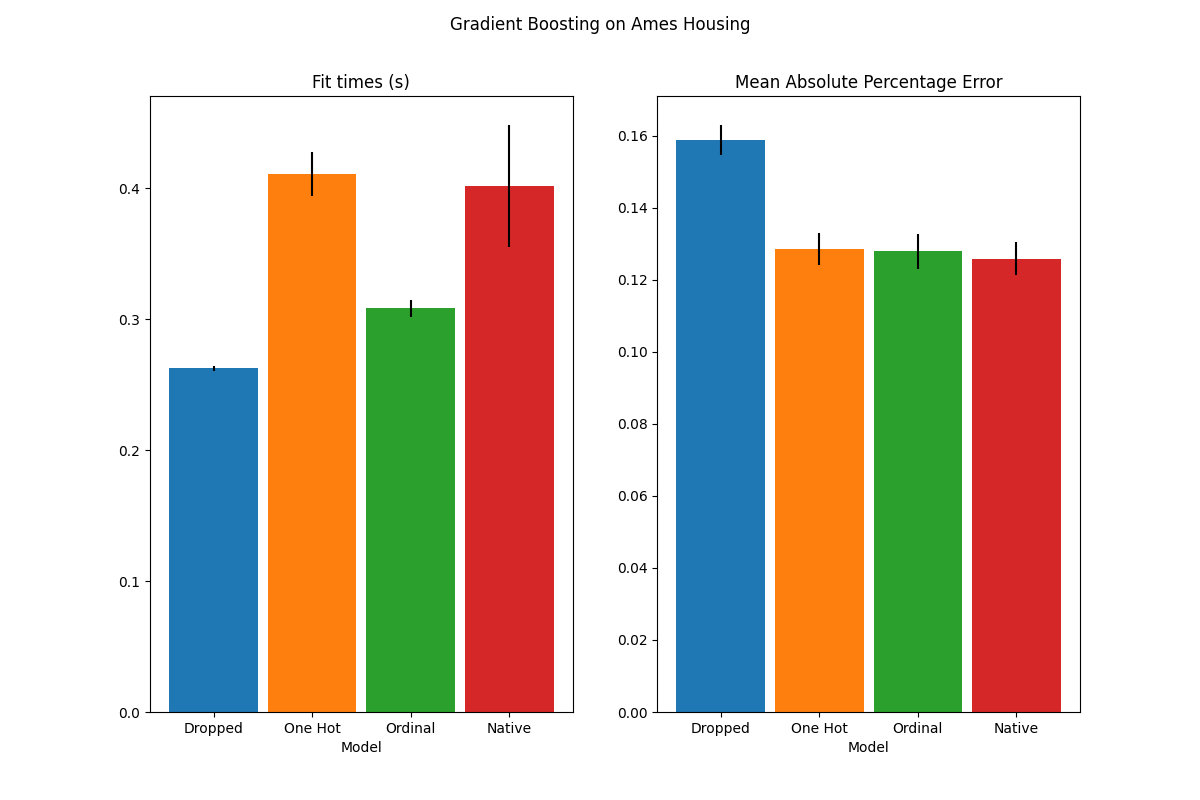
plot_results("Gradient Boosting on Ames Housing")
plot_results("Gradient Boosting on Ames Housing")

• 
• 

نرى أن النموذج الذي يحتوي على بيانات الترميز أحادي الساخن هو الأبطأ على الإطلاق. هذا متوقع، حيث أن الترميز أحادي الساخن ينشئ ميزة إضافية واحدة لكل قيمة فئة (لكل ميزة تصنيفية)، وبالتالي هناك حاجة إلى المزيد من نقاط الانقسام للنظر فيها أثناء التجهيز. من الناحية النظرية، نتوقع أن يكون التعامل الأصلي مع الميزات التصنيفية أبطأ قليلاً من معاملة الفئات على أنها كميات مرتبة ('Ordinal')، حيث يتطلب التعامل الأصلي فرز الفئات. يجب أن تكون أوقات التجهيز قريبة عندما يكون عدد الفئات صغيرًا، وقد لا ينعكس ذلك دائمًا في الممارسة العملية.

من حيث أداء التنبؤ، يؤدي إسقاط الميزات التصنيفية إلى أداء أضعف. تمتلك النماذج الثلاثة التي تستخدم الميزات التصنيفية معدلات خطأ قابلة للمقارنة، مع ميزة طفيفة للتعامل الأصلي.

تحديد عدد الانقسامات

بشكل عام، يمكن توقع تنبؤات أضعف من البيانات ذات الترميز أحادي الساخن، خاصة عندما تكون أعماق الأشجار أو عدد العقد محدودة: مع البيانات ذات الترميز أحادي الساخن، هناك حاجة إلى المزيد من نقاط الانقسام، أي المزيد من العمق، من أجل استعادة انقسام مكافئ يمكن الحصول عليه في نقطة انقسام واحدة مع التعامل الأصلي.

هذا صحيح أيضًا عندما يتم التعامل مع الفئات على أنها كميات ترتيبية: إذا كانت الفئات A..F والانقسام الأفضل هو ACF - BDE، فإن النموذج الذي يستخدم الترميز أحادي الساخن سيحتاج إلى 3 نقاط انقسام (واحدة لكل فئة في العقدة اليسرى)، والنموذج غير الأصلي الترتيبي سيحتاج إلى 4 انقسامات: 1 انقسام لعزل A، 1 انقسام لعزل F، و2 انقسامات لعزل C من BCDE.

يعتمد مدى اختلاف أداء النماذج في الممارسة العملية على مجموعة البيانات وعلى مرونة الأشجار.

لرؤية ذلك، دعنا نعيد تشغيل نفس التحليل مع نماذج غير ملائمة حيث نقوم بشكل مصطنع بتحديد العدد الإجمالي للانقسامات من خلال تحديد عدد الأشجار وعمق كل شجرة.

for pipe in (hist_dropped, hist_one_hot, hist_ordinal, hist_native):
    if pipe is hist_native:
        # النموذج الأصلي لا يستخدم خط أنابيب لذا، يمكننا تعيين المعلمات
        # مباشرة.
        pipe.set_params(max_depth=3, max_iter=15)
    else:
        pipe.set_params(
            histgradientboostingregressor__max_depth=3,
            histgradientboostingregressor__max_iter=15,
        )

dropped_result = cross_validate(hist_dropped, X, y, cv=n_cv_folds, scoring=scoring)
one_hot_result = cross_validate(hist_one_hot, X, y, cv=n_cv_folds, scoring=scoring)
ordinal_result = cross_validate(hist_ordinal, X, y, cv=n_cv_folds, scoring=scoring)
native_result = cross_validate(hist_native, X, y, cv=n_cv_folds, scoring=scoring)

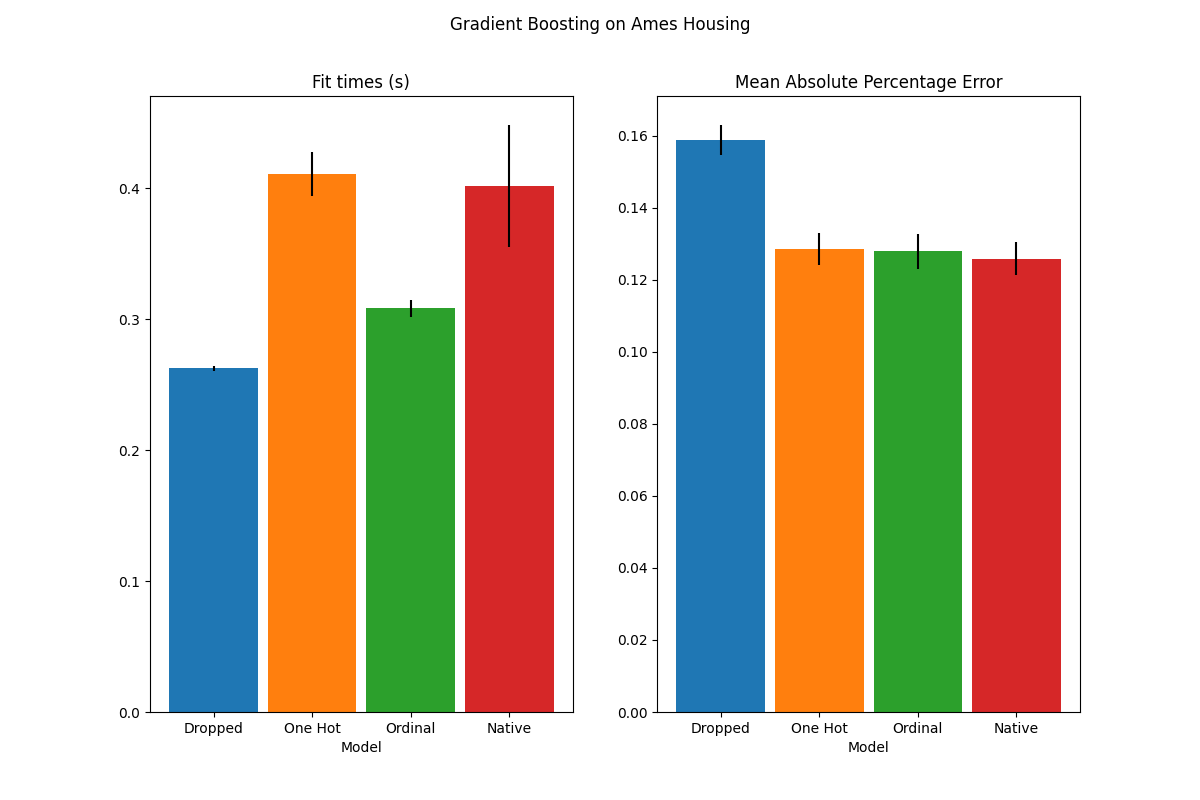
plot_results("Gradient Boosting on Ames Housing (few and small trees)")

plt.show()

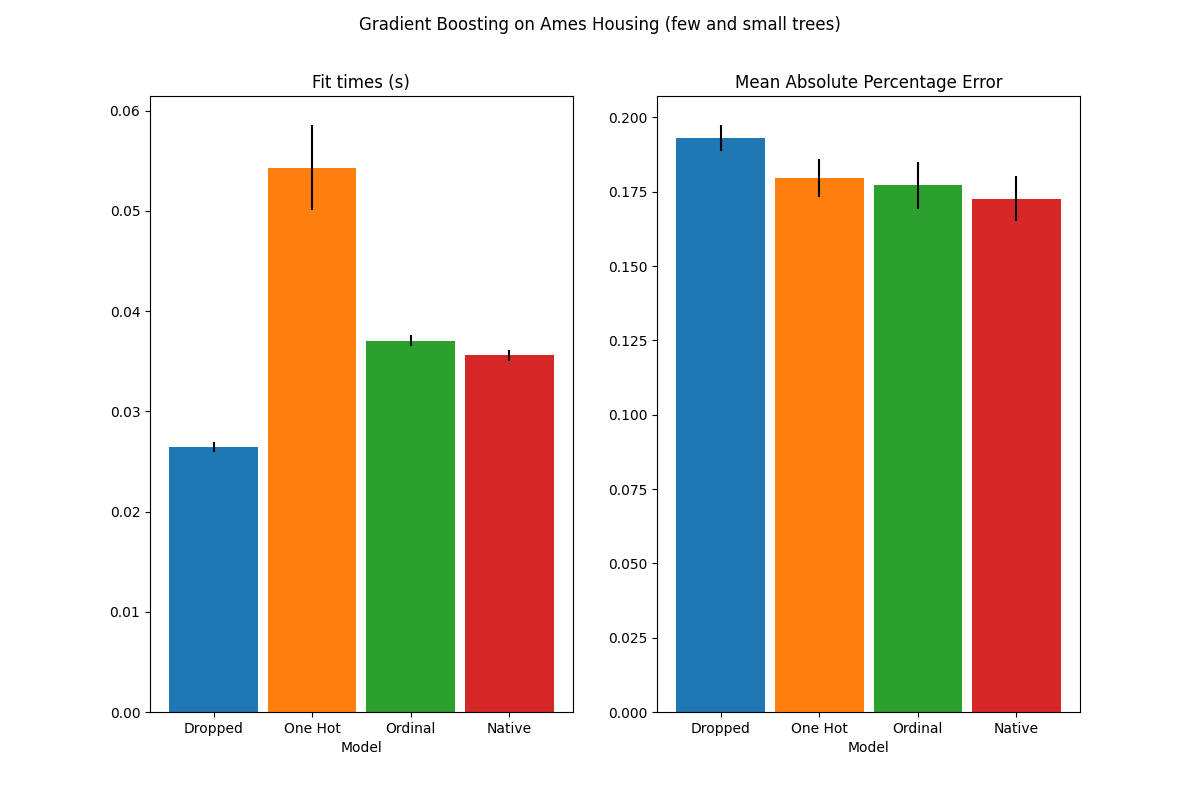
تؤكد نتائج هذه النماذج غير الملائمة حدسنا السابق: استراتيجية التعامل مع الفئات الأصلية تؤدي الأداء الأفضل عندما تكون ميزانية الانقسام مقيدة. تؤدي الاستراتيجيتان الأخريان (الترميز أحادي الساخن ومعاملة الفئات على أنها قيم ترتيبية) إلى قيم خطأ قابلة للمقارنة مع النموذج الأساسي الذي أسقط الميزات التصنيفية تمامًا.

Related examples

مقارنة ترميز الهدف مع الترميزات الأخرى

مقارنة ترميز الهدف مع الترميزات الأخرى

أبرز ميزات الإصدار 0.24 من scikit-learn

أبرز ميزات الإصدار 0.24 من scikit-learn

دمج المتنبئات باستخدام التكديس

دمج المتنبئات باستخدام التكديس

هندسة الميزات ذات الصلة بالوقت

هندسة الميزات ذات الصلة بالوقت