ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

منحنيات معايرة الاحتمالية#

عند إجراء التصنيف، غالبًا ما يرغب المرء في التنبؤ ليس فقط بتسمية الفئة، ولكن أيضًا بالاحتمالية المرتبطة بها. يعطي هذا الاحتمال نوعًا من الثقة في التنبؤ. يوضح هذا المثال كيفية تصور مدى جودة معايرة الاحتمالات المتوقعة باستخدام منحنيات المعايرة، والمعروفة أيضًا باسم مخططات الموثوقية. سيتم أيضًا توضيح معايرة مصنف غير معاير.

# المؤلفون: مطورو scikit-learn
# مُعرِّف ترخيص SPDX: BSD-3-Clause

مجموعة البيانات#

سنستخدم مجموعة بيانات تصنيف ثنائية تركيبية مع 100000 عينة و 20 ميزة. من بين الميزات العشرين، هناك 2 فقط غنية بالمعلومات، و 10 زائدة عن الحاجة (مجموعات عشوائية من الميزات الغنية بالمعلومات) و الميزات الثمانية المتبقية غير مفيدة (أرقام عشوائية). من بين 100000 عينة، سيتم استخدام 1000 عينة لملاءمة النموذج والباقي للاختبار.

from sklearn.svm import LinearSVC
import numpy as np
from sklearn.metrics import (
    brier_score_loss,
    f1_score,
    log_loss,
    precision_score,
    recall_score,
    roc_auc_score,
)
import pandas as pd
from collections import defaultdict
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import LogisticRegression
from sklearn.calibration import CalibratedClassifierCV, CalibrationDisplay
from matplotlib.gridspec import GridSpec
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split

X, y = make_classification(
    n_samples=100_000, n_features=20, n_informative=2, n_redundant=10, random_state=42
)

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.99, random_state=42
)

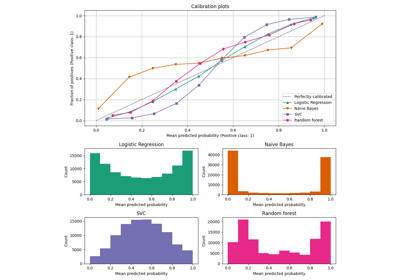
منحنيات المعايرة#

Gaussian Naive Bayes#

أولاً، سنقارن:

LogisticRegression (يُستخدم كخط أساس لأنه في كثير من الأحيان، يكون انحدار لوجستي مُنظَّم بشكل صحيح معايرًا جيدًا افتراضيًا بفضل استخدام فقدان السجل)
GaussianNB غير معاير
GaussianNB مع معايرة متساوية التوتر وسيجمويد (انظر دليل المستخدم)

تم رسم منحنيات المعايرة لجميع الشروط الأربعة أدناه، مع متوسط الاحتمال المتوقع لكل صندوق على المحور السيني ونسبة الفئات الإيجابية في كل صندوق على المحور الصادي.

lr = LogisticRegression(C=1.0)
gnb = GaussianNB()
gnb_isotonic = CalibratedClassifierCV(gnb, cv=2, method="isotonic")
gnb_sigmoid = CalibratedClassifierCV(gnb, cv=2, method="sigmoid")

clf_list = [
    (lr, "الانحدار اللوجستي"),
    (gnb, "Naive Bayes"),
    (gnb_isotonic, "Naive Bayes + متساوي التوتر"),
    (gnb_sigmoid, "Naive Bayes + سيجمويد"),
]

fig = plt.figure(figsize=(10, 10))
gs = GridSpec(4, 2)
colors = plt.get_cmap("Dark2")

ax_calibration_curve = fig.add_subplot(gs[:2, :2])
calibration_displays = {}
for i, (clf, name) in enumerate(clf_list):
    clf.fit(X_train, y_train)
    display = CalibrationDisplay.from_estimator(
        clf,
        X_test,
        y_test,
        n_bins=10,
        name=name,
        ax=ax_calibration_curve,
        color=colors(i),
    )
    calibration_displays[name] = display

ax_calibration_curve.grid()
ax_calibration_curve.set_title("مخططات المعايرة (Naive Bayes)")

# إضافة الرسم البياني
grid_positions = [(2, 0), (2, 1), (3, 0), (3, 1)]
for i, (_, name) in enumerate(clf_list):
    row, col = grid_positions[i]
    ax = fig.add_subplot(gs[row, col])

    ax.hist(
        calibration_displays[name].y_prob,
        range=(0, 1),
        bins=10,
        label=name,
        color=colors(i),
    )
    ax.set(title=name, xlabel="متوسط ​​الاحتمال المتوقع", ylabel="العدد")

plt.tight_layout()
plt.show()

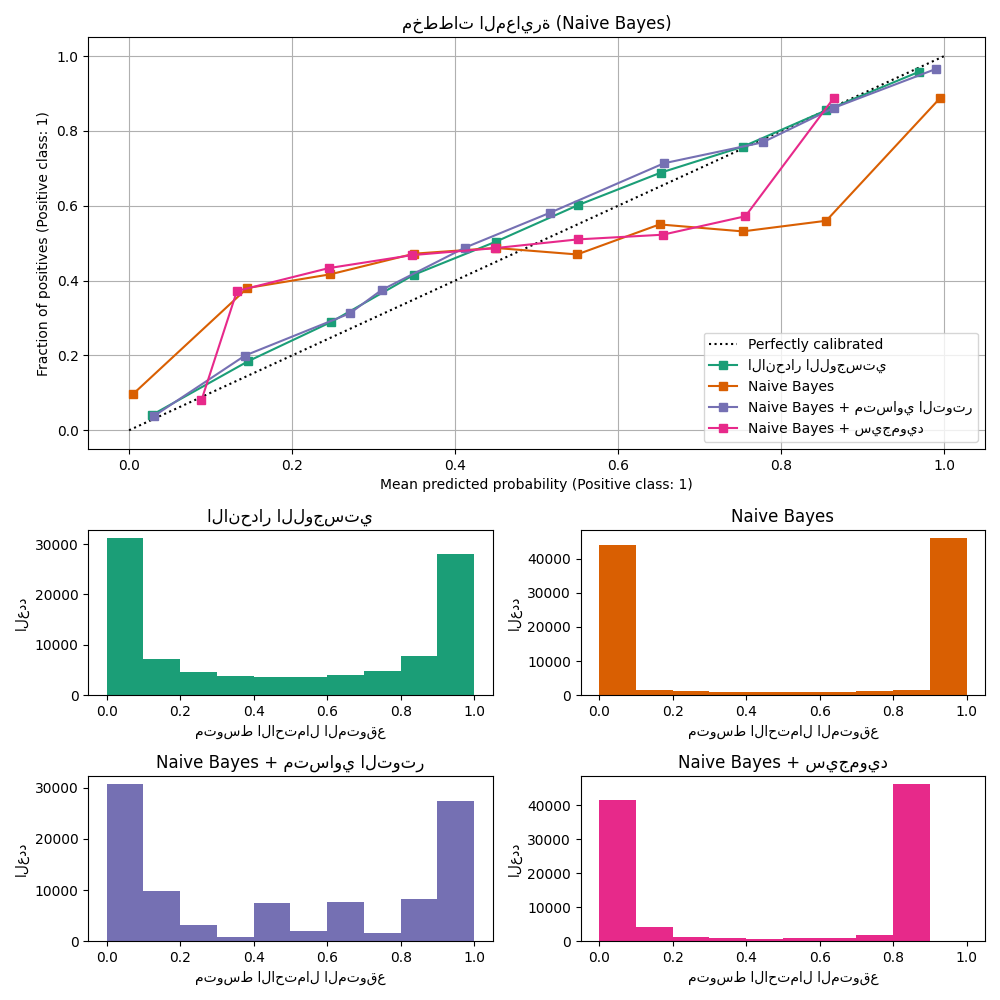
مخططات المعايرة (Naive Bayes), الانحدار اللوجستي, Naive Bayes, Naive Bayes + متساوي التوتر, Naive Bayes + سيجمويد

GaussianNB غير المعاير معاير بشكل سيئ بسبب الميزات الزائدة عن الحاجة التي تنتهك افتراض استقلال الميزات وتؤدي إلى مصنف مفرط الثقة، وهو ما يُشار إليه بواسطة منحنى سيجمويد المنقول النموذجي. يمكن أن تُعالج معايرة الاحتمالات لـ GaussianNB باستخدام الانحدار المتساوي التوتر هذه المشكلة كما يتضح من منحنى المعايرة القطري تقريبًا. انحدار سيجمويد يُحسِّن أيضًا المعايرة قليلاً، وإن لم يكن بنفس قوة الانحدار المتساوي التوتر غير المعياري. يمكن أن يُعزى ذلك إلى حقيقة أن لدينا الكثير من بيانات المعايرة بحيث يمكن استغلال مرونة أكبر للنموذج غير المعياري.

أدناه، سنقوم بإجراء تحليل كمي مع الأخذ في الاعتبار العديد من مقاييس التصنيف: خسارة درجة بريير، خسارة السجل، الدقة، الاستدعاء، درجة F1 و ROC AUC.

scores = defaultdict(list)
for i, (clf, name) in enumerate(clf_list):
    clf.fit(X_train, y_train)
    y_prob = clf.predict_proba(X_test)
    y_pred = clf.predict(X_test)
    scores["المصنف"].append(name)

    for metric in [brier_score_loss, log_loss, roc_auc_score]:
        score_name = metric.__name__.replace(
            "_", " ").replace("score", "").capitalize()
        scores[score_name].append(metric(y_test, y_prob[:, 1]))

    for metric in [precision_score, recall_score, f1_score]:
        score_name = metric.__name__.replace(
            "_", " ").replace("score", "").capitalize()
        scores[score_name].append(metric(y_test, y_pred))

    score_df = pd.DataFrame(scores).set_index("المصنف")
    score_df.round(decimals=3)

score_df

	Brier loss	Log loss	Roc auc	Precision	Recall	F1
المصنف
الانحدار اللوجستي	0.098932	0.323200	0.937443	0.871965	0.851348	0.861533
Naive Bayes	0.117608	0.782755	0.940374	0.857400	0.875941	0.866571
Naive Bayes + متساوي التوتر	0.098332	0.370738	0.938613	0.883065	0.836224	0.859007
Naive Bayes + سيجمويد	0.108880	0.368896	0.940201	0.861106	0.871277	0.866161

لاحظ أنه على الرغم من أن المعايرة تُحسِّن خسارة درجة بريير (مقياس يتكون من مصطلح المعايرة ومصطلح التحسين) و خسارة السجل، فإنها لا تُغيِّر مقاييس دقة التنبؤ (الدقة والاستدعاء و درجة F1) بشكل كبير. وذلك لأن المعايرة يجب ألا تُغيِّر احتمالات التنبؤ بشكل كبير في موقع عتبة القرار (عند x = 0.5 على الرسم البياني). ومع ذلك، يجب أن تجعل المعايرة احتمالات التنبؤ أكثر دقة وبالتالي أكثر فائدة لاتخاذ قرارات التخصيص في ظل عدم اليقين. علاوة على ذلك، يجب ألا يتغير ROC AUC على الإطلاق لأن المعايرة هي تحويل رتيب. في الواقع، لا تتأثر مقاييس الرتبة بالمعايرة.

مُصنِّف متجه الدعم الخطي#

بعد ذلك، سنقارن:

LogisticRegression (الخط الأساسي)
LinearSVC غير معاير. نظرًا لأن SVC لا يُخرج الاحتمالات افتراضيًا، فإننا نقوم بتغيير نطاق ناتج decision_function بسذاجة إلى [0، 1] عن طريق تطبيق تغيير نطاق الحد الأدنى-الحد الأقصى.
LinearSVC مع معايرة متساوية التوتر وسيجمويد (انظر دليل المستخدم)

class NaivelyCalibratedLinearSVC(LinearSVC):
    """LinearSVC مع أسلوب `predict_proba` الذي يُغيِّر نطاق
    ناتج `decision_function` بسذاجة للتصنيف الثنائي."""

    def fit(self, X, y):
        super().fit(X, y)
        df = self.decision_function(X)
        self.df_min_ = df.min()
        self.df_max_ = df.max()

    def predict_proba(self, X):
        """تغيير نطاق ناتج `decision_function` من الحد الأدنى للحد الأقصى إلى [0، 1]."""
        df = self.decision_function(X)
        calibrated_df = (df - self.df_min_) / (self.df_max_ - self.df_min_)
        proba_pos_class = np.clip(calibrated_df, 0, 1)
        proba_neg_class = 1 - proba_pos_class
        proba = np.c_[proba_neg_class, proba_pos_class]
        return proba

lr = LogisticRegression(C=1.0)
svc = NaivelyCalibratedLinearSVC(max_iter=10_000)
svc_isotonic = CalibratedClassifierCV(svc, cv=2, method="isotonic")
svc_sigmoid = CalibratedClassifierCV(svc, cv=2, method="sigmoid")

clf_list = [
    (lr, "الانحدار اللوجستي"),
    (svc, "SVC"),
    (svc_isotonic, "SVC + متساوي التوتر"),
    (svc_sigmoid, "SVC + سيجمويد"),
]

fig = plt.figure(figsize=(10, 10))
gs = GridSpec(4, 2)

ax_calibration_curve = fig.add_subplot(gs[:2, :2])
calibration_displays = {}
for i, (clf, name) in enumerate(clf_list):
    clf.fit(X_train, y_train)
    display = CalibrationDisplay.from_estimator(
        clf,
        X_test,
        y_test,
        n_bins=10,
        name=name,
        ax=ax_calibration_curve,
        color=colors(i),
    )
    calibration_displays[name] = display

ax_calibration_curve.grid()
ax_calibration_curve.set_title("مخططات المعايرة (SVC)")

# إضافة الرسم البياني
grid_positions = [(2, 0), (2, 1), (3, 0), (3, 1)]
for i, (_, name) in enumerate(clf_list):
    row, col = grid_positions[i]
    ax = fig.add_subplot(gs[row, col])

    ax.hist(
        calibration_displays[name].y_prob,
        range=(0, 1),
        bins=10,
        label=name,
        color=colors(i),
    )
    ax.set(title=name, xlabel="متوسط ​​الاحتمال المتوقع", ylabel="العدد")

plt.tight_layout()
plt.show()

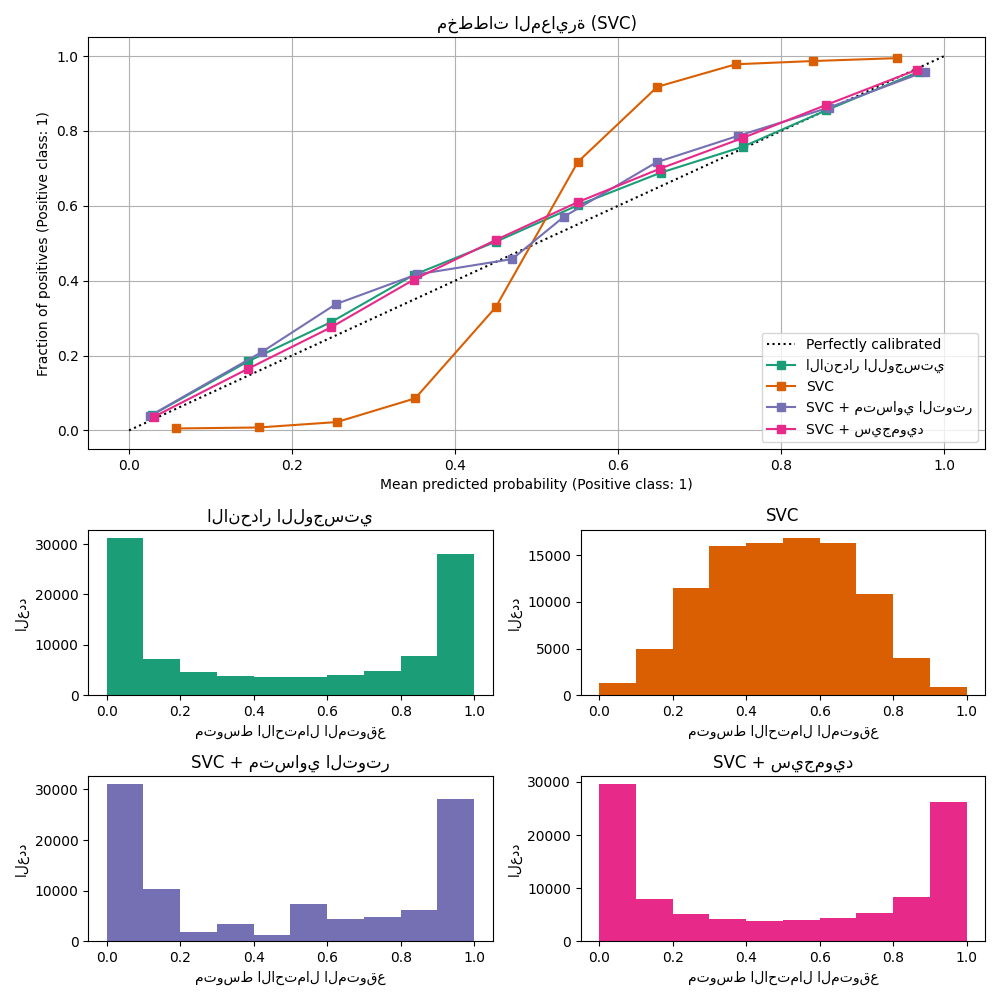
مخططات المعايرة (SVC), الانحدار اللوجستي, SVC, SVC + متساوي التوتر, SVC + سيجمويد

يُظهر LinearSVC سلوكًا معاكسًا لـ GaussianNB؛ منحنى المعايرة له شكل سيجمويد، وهو نموذجي لمصنف غير واثق. في حالة LinearSVC، يحدث هذا بسبب خاصية الهامش لفقدان المفصلة، التي تُركز على العينات القريبة من حد القرار (متجهات الدعم). لا تؤثر العينات البعيدة عن حد القرار على فقدان المفصلة. وبالتالي، فمن المنطقي أن LinearSVC لا يحاول فصل العينات في مناطق منطقة الثقة العالية. يؤدي هذا إلى تسطيح منحنيات المعايرة بالقرب من 0 و 1 ويظهر تجريبيًا مع مجموعة متنوعة من مجموعات البيانات في Niculescu-Mizil & Caruana [1].

يمكن لكلا النوعين من المعايرة (سيجمويد ومتساوي التوتر) إصلاح هذه المشكلة وتحقيق نتائج مماثلة.

كما كان من قبل، نعرض خسارة درجة بريير، خسارة السجل، الدقة، الاستدعاء، درجة F1 و ROC AUC.

scores = defaultdict(list)
for i, (clf, name) in enumerate(clf_list):
    clf.fit(X_train, y_train)
    y_prob = clf.predict_proba(X_test)
    y_pred = clf.predict(X_test)
    scores["المصنف"].append(name)

    for metric in [brier_score_loss, log_loss, roc_auc_score]:
        score_name = metric.__name__.replace(
            "_", " ").replace("score", "").capitalize()
        scores[score_name].append(metric(y_test, y_prob[:, 1]))

    for metric in [precision_score, recall_score, f1_score]:
        score_name = metric.__name__.replace(
            "_", " ").replace("score", "").capitalize()
        scores[score_name].append(metric(y_test, y_pred))

    score_df = pd.DataFrame(scores).set_index("المصنف")
    score_df.round(decimals=3)

score_df

	Brier loss	Log loss	Roc auc	Precision	Recall	F1
المصنف
الانحدار اللوجستي	0.098932	0.323200	0.937443	0.871965	0.851348	0.861533
SVC	0.144943	0.465660	0.937597	0.872186	0.851792	0.861868
SVC + متساوي التوتر	0.099820	0.376999	0.936480	0.853174	0.877981	0.865400
SVC + سيجمويد	0.098758	0.321301	0.937532	0.873724	0.848743	0.861053

كما هو الحال مع GaussianNB أعلاه، تُحسِّن المعايرة كلاً من خسارة درجة بريير و خسارة السجل ولكنها لا تُغيِّر مقاييس دقة التنبؤ (الدقة والاستدعاء ودرجة F1) كثيرًا.

الملخص#

يمكن أن تتعامل معايرة سيجمويد المعلمية مع المواقف التي يكون فيها منحنى المعايرة للمصنف الأساسي سيجمويد (على سبيل المثال، لـ LinearSVC) ولكن ليس عندما يكون سيجمويد منقول (على سبيل المثال، GaussianNB). يمكن للمعايرة المتساوية التوتر غير المعلمية التعامل مع كلا الموقفين ولكنها قد تتطلب المزيد من البيانات لإنتاج نتائج جيدة.