ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

تأثير تنظيم النموذج على خطأ التدريب والاختبار#

في هذا المثال، نقيم تأثير معامل التنظيم في نموذج خطي يسمى ElasticNet. ولإجراء هذا التقييم، نستخدم منحنى التحقق باستخدام ValidationCurveDisplay. يُظهر هذا المنحنى درجات التدريب والاختبار للنموذج لقيم مختلفة لمعامل التنظيم.

بمجرد تحديد معامل التنظيم الأمثل، نقارن المعاملات الحقيقية والمقدرة للنموذج لتحديد ما إذا كان النموذج قادرًا على استرداد المعاملات من بيانات الإدخال المشوشة.

# المؤلفون: مطوري سكايلرن
# معرف الترخيص: BSD-3-Clause

توليد بيانات العينة#

نولد مجموعة بيانات انحدار تحتوي على العديد من الميزات النسبية لعدد العينات. ومع ذلك، فإن 10% فقط من الميزات هي ميزات مفيدة. في هذا السياق، تستخدم النماذج الخطية التي تعرض عقوبة L1 بشكل شائع لاسترداد مجموعة متفرقة من المعاملات.

from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split

n_samples_train, n_samples_test, n_features = 150, 300, 500
X, y, true_coef = make_regression(
    n_samples=n_samples_train + n_samples_test,
    n_features=n_features,
    n_informative=50,
    shuffle=False,
    noise=1.0,
    coef=True,
    random_state=42,
)
X_train, X_test, y_train, y_test = train_test_split(
    X, y, train_size=n_samples_train, test_size=n_samples_test, shuffle=False
)

تعريف النموذج#

هنا، لا نستخدم نموذجًا يعرض عقوبة L1 فقط. بدلاً من ذلك، نستخدم نموذج ElasticNet الذي يعرض كل من عقوبات L1 و L2

نقوم بتثبيت معامل l1_ratio بحيث تكون الحل الذي يجده النموذج لا يزال متفرق. لذلك، يحاول هذا النوع من النماذج إيجاد حل متفرق ولكن في نفس الوقت يحاول أيضًا تقليص جميع المعاملات إلى الصفر.

بالإضافة إلى ذلك، نجبر معاملات النموذج على أن تكون إيجابية لأننا نعلم أن make_regression يولد استجابة بإشارة إيجابية. لذا نستخدم هذه المعرفة المسبقة للحصول على نموذج أفضل.

from sklearn.linear_model import ElasticNet

enet = ElasticNet(l1_ratio=0.9, positive=True, max_iter=10_000)

تقييم تأثير معامل التنظيم#

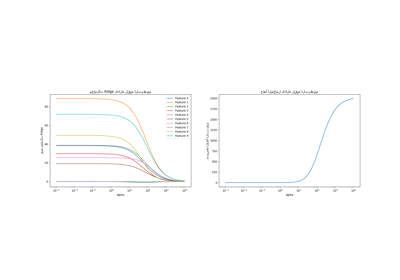
لتقييم تأثير معامل التنظيم، نستخدم منحنى التحقق. يُظهر هذا المنحنى درجات التدريب والاختبار للنموذج لقيم مختلفة لمعامل التنظيم.

معامل التنظيم alpha هو معامل يطبق على معاملات النموذج: عندما يميل إلى الصفر، لا يتم تطبيق أي تنظيم ويحاول النموذج ملاءمة بيانات التدريب مع أقل قدر من الخطأ. ومع ذلك، يؤدي ذلك إلى الإفراط في الملاءمة عندما تكون الميزات مشوشة. عندما يزيد alpha، يتم تقييد معاملات النموذج، وبالتالي لا يستطيع النموذج ملاءمة بيانات التدريب عن كثب، مما يتجنب الإفراط في الملاءمة. ومع ذلك، إذا تم تطبيق الكثير من التنظيم، فإن النموذج لا يلائم البيانات بشكل كافٍ ولا يستطيع التقاط الإشارة بشكل صحيح.

يساعد منحنى التحقق في إيجاد توازن جيد بين كلا الطرفين: النموذج غير منظم وبالتالي مرن بما يكفي لملاءمة الإشارة، ولكن ليس مرنًا للغاية لدرجة الإفراط في الملاءمة. يسمح لنا ValidationCurveDisplay بعرض درجات التدريب والتحقق عبر نطاق من قيم alpha

import numpy as np

from sklearn.model_selection import ValidationCurveDisplay

alphas = np.logspace(-5, 1, 60)
disp = ValidationCurveDisplay.from_estimator(
    enet,
    X_train,
    y_train,
    param_name="alpha",
    param_range=alphas,
    scoring="r2",
    n_jobs=2,
    score_type="both",
)
disp.ax_.set(
    title=r"منحنى التحقق لنموذج ElasticNet (R$^2$ Score)",
    xlabel=r"alpha (قوة التنظيم)",
    ylabel="R$^2$ Score",
)

test_scores_mean = disp.test_scores.mean(axis=1)
idx_avg_max_test_score = np.argmax(test_scores_mean)
disp.ax_.vlines(
    alphas[idx_avg_max_test_score],
    disp.ax_.get_ylim()[0],
    test_scores_mean[idx_avg_max_test_score],
    color="k",
    linewidth=2,
    linestyle="--",
    label=f"Optimum on test\n$\\alpha$ = {alphas[idx_avg_max_test_score]:.2e}",
)
_ = disp.ax_.legend(loc="lower right")

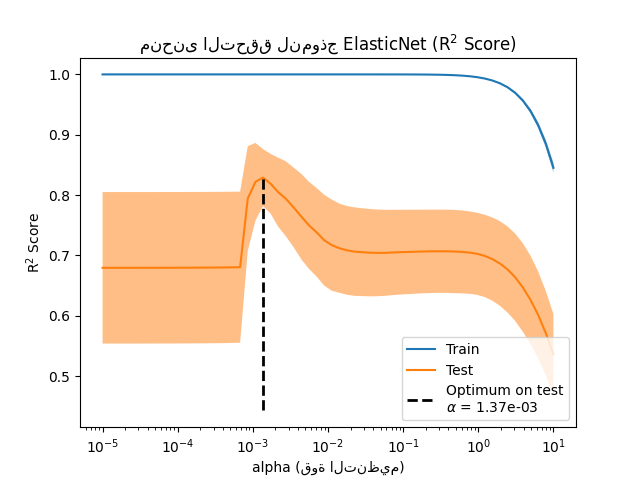
منحنى التحقق لنموذج ElasticNet (R$^2$ Score)

لإيجاد معامل التنظيم الأمثل، يمكننا اختيار قيمة alpha التي تعظم درجة التحقق.

مقارنة المعاملات#

الآن بعد أن حددنا معامل التنظيم الأمثل، يمكننا مقارنة المعاملات الحقيقية والمقدرة.

أولاً، دعنا نحدد معامل التنظيم إلى القيمة المثلى ونلائم النموذج على بيانات التدريب. بالإضافة إلى ذلك، سنعرض درجة الاختبار لهذا النموذج.

enet.set_params(alpha=alphas[idx_avg_max_test_score]).fit(X_train, y_train)
print(
    f"Test score: {enet.score(X_test, y_test):.3f}",
)

Test score: 0.884

الآن، نرسم المعاملات الحقيقية والمقدرة.

import matplotlib.pyplot as plt

fig, axs = plt.subplots(ncols=2, figsize=(12, 6), sharex=True, sharey=True)
for ax, coef, title in zip(axs, [true_coef, enet.coef_], ["True", "Model"]):
    ax.stem(coef)
    ax.set(
        title=f"{title} Coefficients",
        xlabel="Feature Index",
        ylabel="Coefficient Value",
    )
fig.suptitle(
    "مقارنة معاملات النموذج الحقيقي والمولد\n"
    "معاملات نموذج الشبكة المرنة المقدرة"
)

plt.show()

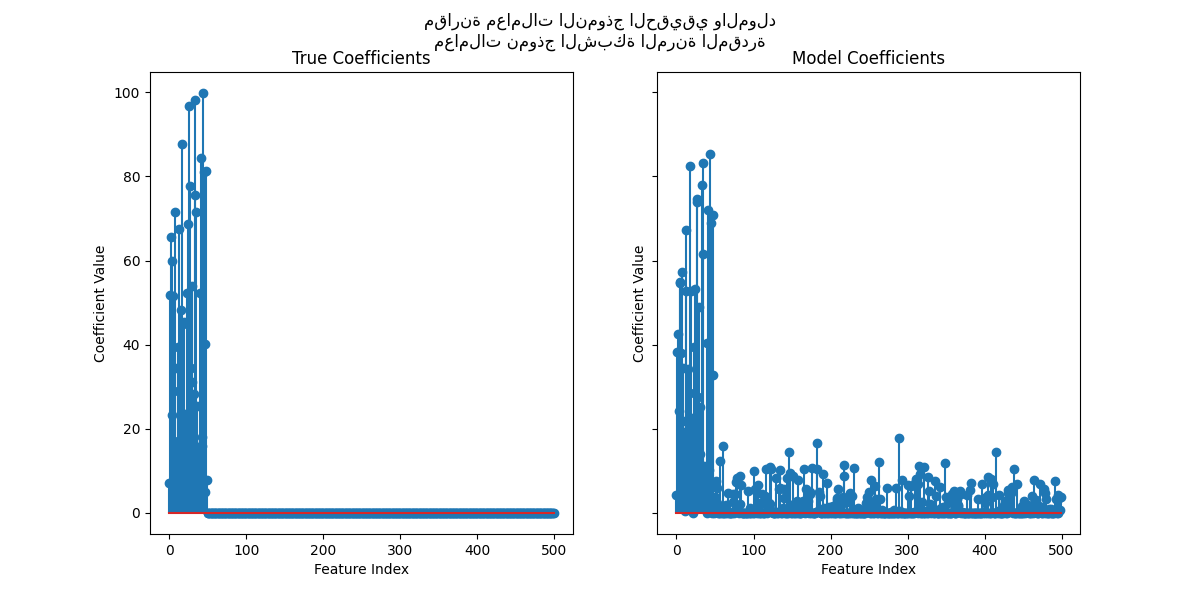
مقارنة معاملات النموذج الحقيقي والمولد معاملات نموذج الشبكة المرنة المقدرة, True Coefficients, Model Coefficients

في حين أن المعاملات الأصلية متفرقة، فإن المعاملات المقدرة ليست متفرقة كما ينبغي. والسبب هو أننا ثبتنا معامل l1_ratio إلى 0.9. يمكننا إجبار النموذج على الحصول على حل أكثر تفرقاً عن طريق زيادة معامل l1_ratio.

ومع ذلك، لاحظنا أنه بالنسبة للمعاملات المقدرة التي تقترب من الصفر في النموذج المولد الحقيقي، فإن نموذجنا يقلصها نحو الصفر. لذلك لا نستعيد المعاملات الحقيقية، ولكننا نحصل على نتيجة منطقية تتماشى مع الأداء الذي تم الحصول عليه على مجموعة الاختبار.

Total running time of the script: (0 minutes 6.162 seconds)