ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

توضيح افتراضات خوارزمية كاي-مينز#

هذا المثال يهدف إلى توضيح المواقف التي تنتج فيها خوارزمية كاي-مينز (k-means) تجميعات غير بديهية وربما غير مرغوب فيها.

# المؤلفون: مطوّرو سكايلرن (scikit-learn)
# معرف رخصة SPDX: BSD-3-Clause

توليد البيانات#

الدالة make_blobs تقوم بتوليد كتل غاوسية متساوية (كروية). للحصول على كتل غاوسية غير متساوية (إهليلجية)، يجب تحديد 'transformation' خطي.

import numpy as np

from sklearn.datasets import make_blobs

n_samples = 1500
random_state = 170
transformation = [[0.60834549, -0.63667341], [-0.40887718, 0.85253229]]

X, y = make_blobs(n_samples=n_samples, random_state=random_state)
X_aniso = np.dot(X, transformation)  # كتل غير متساوية
X_varied, y_varied = make_blobs(
    n_samples=n_samples, cluster_std=[1.0, 2.5, 0.5], random_state=random_state
)  # تباين غير متساوٍ
X_filtered = np.vstack(
    (X[y == 0][:500], X[y == 1][:100], X[y == 2][:10])
)  # كتل بأحجام غير متساوية
y_filtered = [0] * 500 + [1] * 100 + [2] * 10

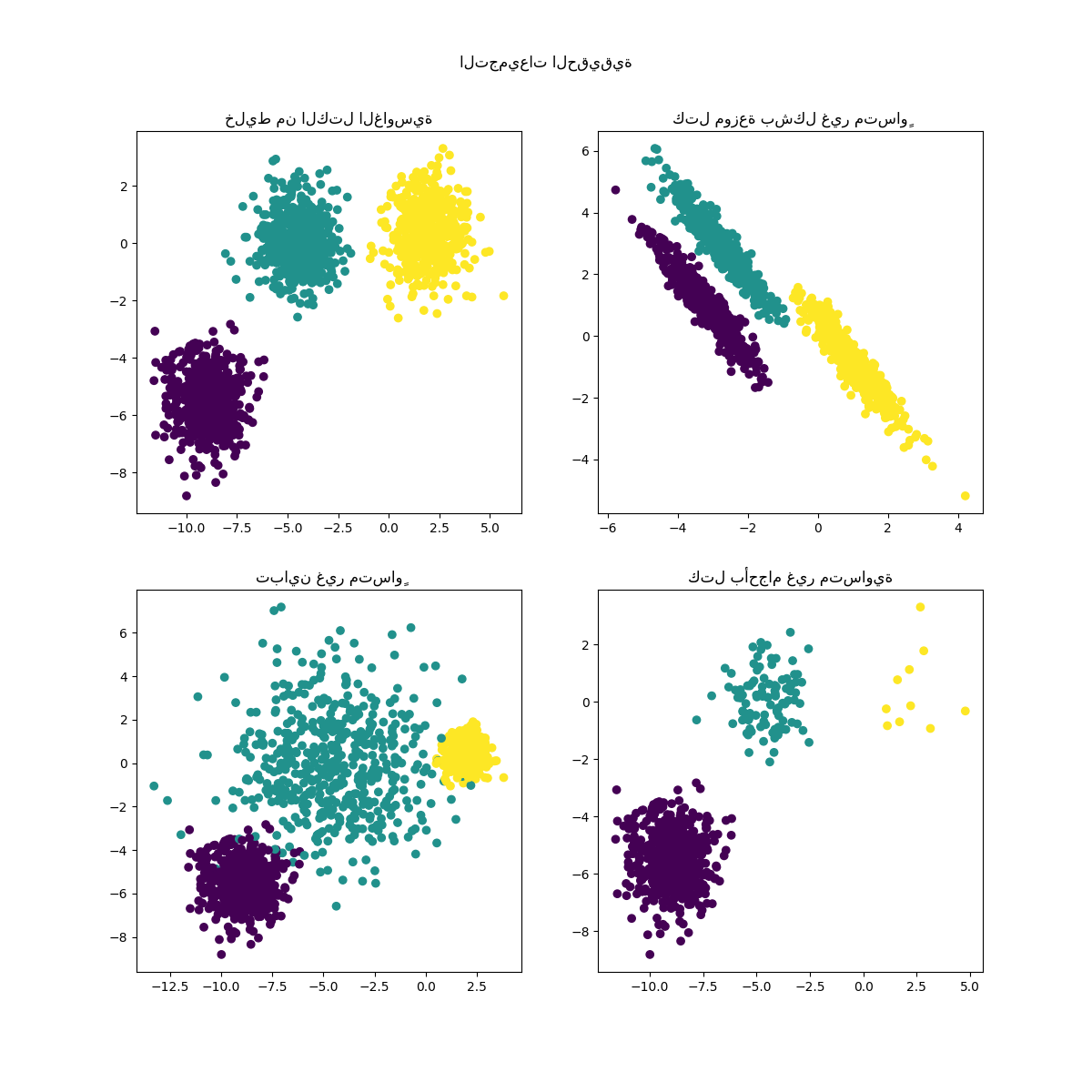
يمكننا تصور البيانات الناتجة:

import matplotlib.pyplot as plt

fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(12, 12))

axs[0, 0].scatter(X[:, 0], X[:, 1], c=y)
axs[0, 0].set_title("خليط من الكتل الغاوسية")

axs[0, 1].scatter(X_aniso[:, 0], X_aniso[:, 1], c=y)
axs[0, 1].set_title("كتل موزعة بشكل غير متساوٍ")

axs[1, 0].scatter(X_varied[:, 0], X_varied[:, 1], c=y_varied)
axs[1, 0].set_title("تباين غير متساوٍ")

axs[1, 1].scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_filtered)
axs[1, 1].set_title("كتل بأحجام غير متساوية")

plt.suptitle("التجميعات الحقيقية").set_y(0.95)
plt.show()

التجميعات الحقيقية, خليط من الكتل الغاوسية, كتل موزعة بشكل غير متساوٍ, تباين غير متساوٍ, كتل بأحجام غير متساوية

ملاءمة النماذج وعرض النتائج#

البيانات المولدة مسبقًا تستخدم الآن لإظهار كيف KMeans يتصرف في السيناريوهات التالية:

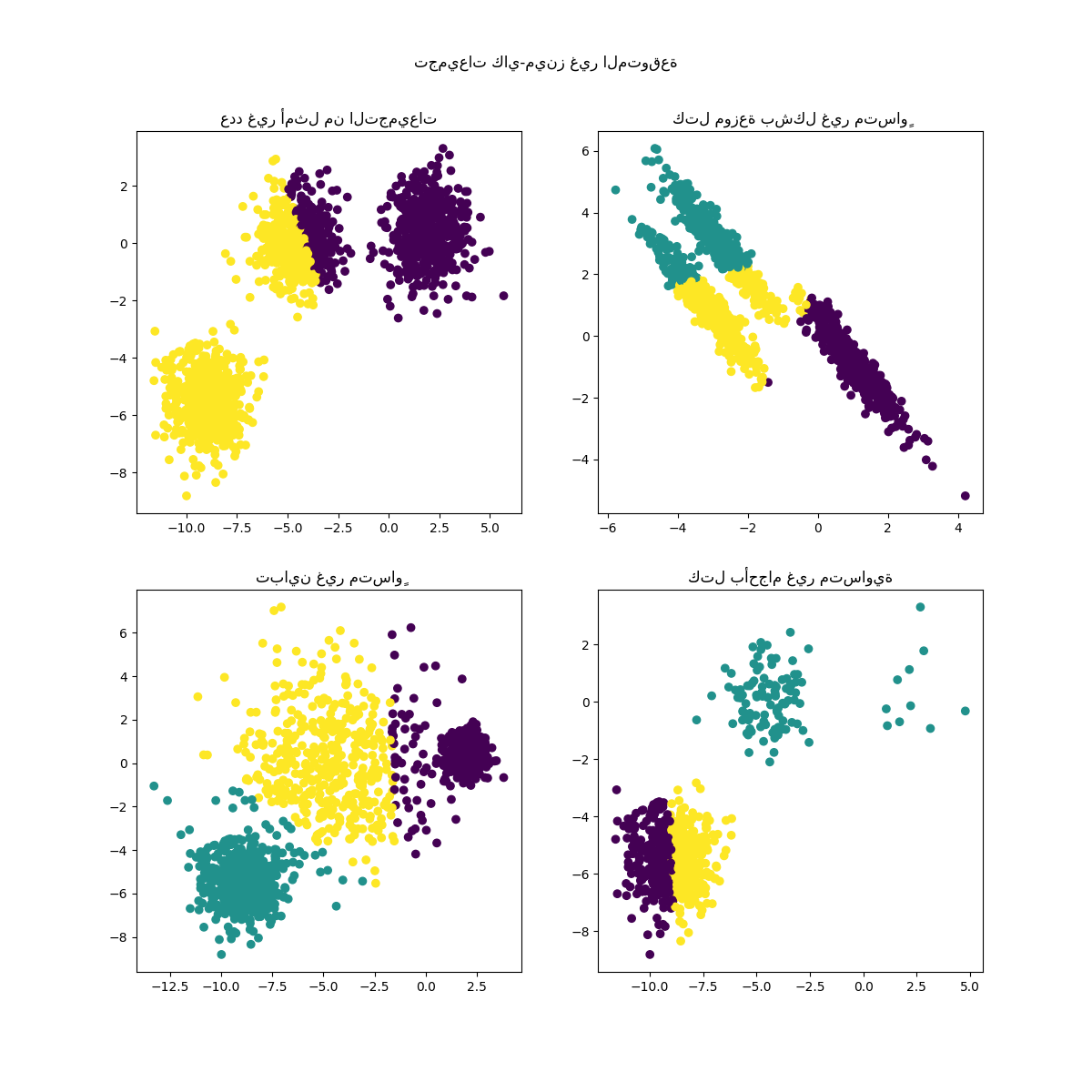
عدد غير أمثل من التجميعات: في الوضع الحقيقي، لا يوجد عدد حقيقي فريد من التجميعات. يجب تحديد عدد مناسب من التجميعات بناءً على معايير قائمة على البيانات ومعرفة الهدف المقصود.
كتل موزعة بشكل غير متساوٍ: تتكون خوارزمية كاي-مينز من تقليل المسافات الإقليدية للعينات إلى مركز التجميع الذي يتم تعيينها إليه. ونتيجة لذلك، تكون خوارزمية كاي-مينز أكثر ملاءمة للتجميعات المتساوية وذات التوزيع الطبيعي (أي الغاوسية الكروية).
تباين غير متساوٍ: خوارزمية كاي-مينز مكافئة لأخذ مقدر الاحتمال الأقصى لمزيج من توزيعات غاوسية k بنفس التباينات ولكن بمتوسطات مختلفة محتملة.
كتل بأحجام غير متساوية: لا توجد نتيجة نظرية حول خوارزمية كاي-مينز تنص على أنها تتطلب أحجامًا متشابهة للتجميعات لتؤدي بشكل جيد، ولكن تقليل المسافات الإقليدية يعني أن المشكلة كلما كانت أكثر ندرة وأبعادها أعلى، كلما زادت الحاجة إلى تشغيل الخوارزمية مع بذور مختلفة للمركز لضمان الحد الأدنى من العطالة العالمية.

from sklearn.cluster import KMeans

common_params = {
    "n_init": "auto",
    "random_state": random_state,
}

fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(12, 12))

y_pred = KMeans(n_clusters=2, **common_params).fit_predict(X)
axs[0, 0].scatter(X[:, 0], X[:, 1], c=y_pred)
axs[0, 0].set_title("عدد غير أمثل من التجميعات")

y_pred = KMeans(n_clusters=3, **common_params).fit_predict(X_aniso)
axs[0, 1].scatter(X_aniso[:, 0], X_aniso[:, 1], c=y_pred)
axs[0, 1].set_title("كتل موزعة بشكل غير متساوٍ")

y_pred = KMeans(n_clusters=3, **common_params).fit_predict(X_varied)
axs[1, 0].scatter(X_varied[:, 0], X_varied[:, 1], c=y_pred)
axs[1, 0].set_title("تباين غير متساوٍ")

y_pred = KMeans(n_clusters=3, **common_params).fit_predict(X_filtered)
axs[1, 1].scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_pred)
axs[1, 1].set_title("كتل بأحجام غير متساوية")

plt.suptitle("تجميعات كاي-مينز غير المتوقعة").set_y(0.95)
plt.show()
plt.suptitle("تجميعات كاي-مينز غير المتوقعة").set_y(0.95)
plt.show()

تجميعات كاي-مينز غير المتوقعة, عدد غير أمثل من التجميعات, كتل موزعة بشكل غير متساوٍ, تباين غير متساوٍ, كتل بأحجام غير متساوية

الحلول الممكنة#

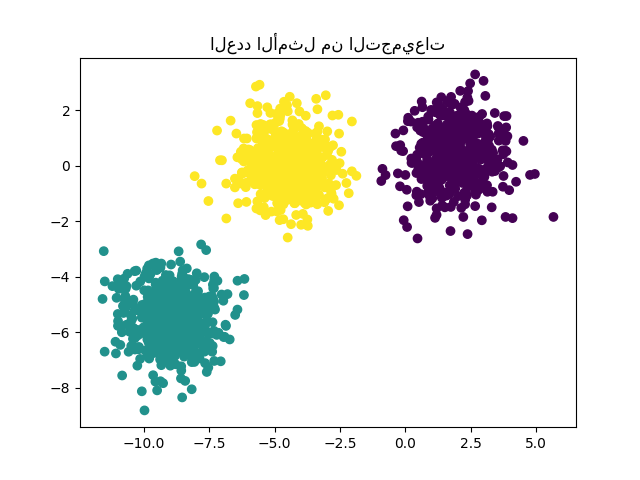
لمثال حول كيفية إيجاد العدد الصحيح من الكتل، راجع تحليل السيلويت لتحديد عدد التجمعات في التجميع التجميعي KMeans. في هذه الحالة، يكفي تعيين 'n_clusters=3'.

y_pred = KMeans(n_clusters=3, **common_params).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.title("العدد الأمثل من التجميعات")
plt.show()

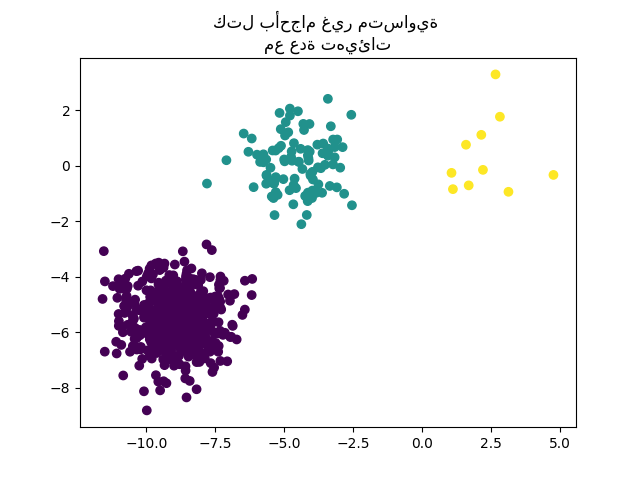
للتعامل مع الكتل ذات الأحجام غير المتساوية، يمكن زيادة عدد التهيئات العشوائية. في هذه الحالة، نحدد 'n_init=10' لتجنب إيجاد الحد الأدنى المحلي غير الأمثل. لمزيد من التفاصيل، راجع تجميع البيانات النادرة باستخدام k-means.

y_pred = KMeans(n_clusters=3, n_init=10, random_state=random_state).fit_predict(
    X_filtered
)
plt.scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_pred)
plt.title("كتل بأحجام غير متساوية \nمع عدة تهيئات")
plt.show()

نظرًا لأن عدم التماثل وعدم المساواة في التباين هي قيود حقيقية لخوارزمية كاي-مينز، نقترح هنا استخدام GaussianMixture، والتي تفترض أيضًا وجود كتل غاوسية ولكنها لا تفرض أي قيود على تبايناتها. لاحظ أنه لا يزال يجب إيجاد العدد الصحيح من الكتل (راجع اختيار نموذج المزيج الغاوسي).

لمثال حول كيفية تعامل طرق التجميع الأخرى مع الكتل غير المتساوية أو ذات التباين غير المتساوي، راجع المثال مقارنة خوارزميات التجميع المختلفة على مجموعات البيانات التجريبية.

from sklearn.mixture import GaussianMixture

fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, figsize=(12, 6))

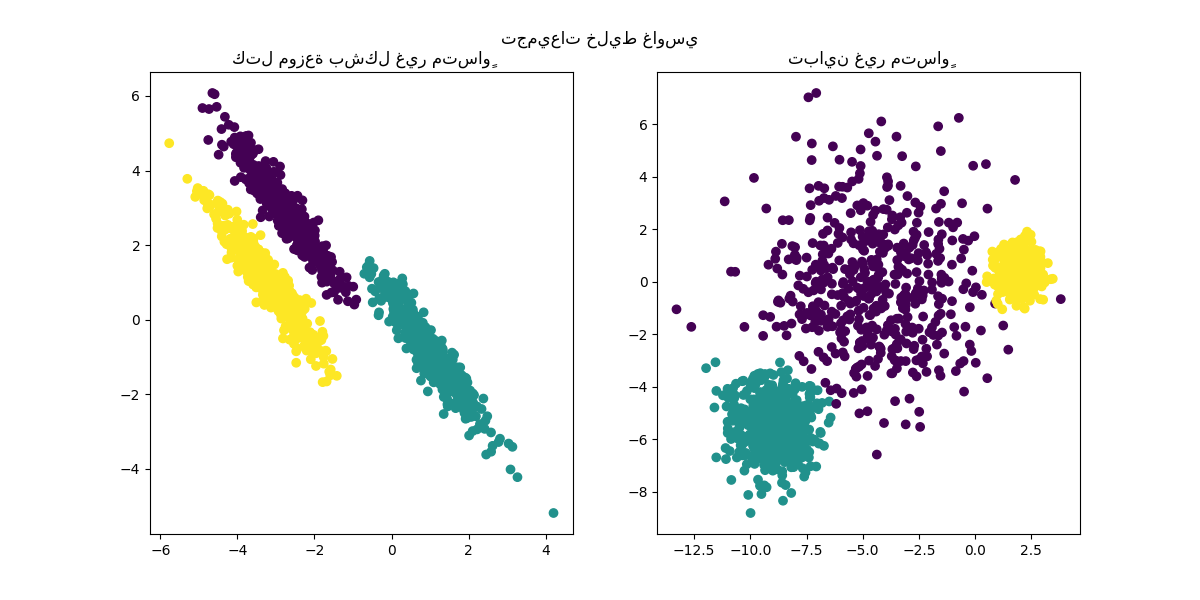
y_pred = GaussianMixture(n_components=3).fit_predict(X_aniso)
ax1.scatter(X_aniso[:, 0], X_aniso[:, 1], c=y_pred)
ax1.set_title("كتل موزعة بشكل غير متساوٍ")

y_pred = GaussianMixture(n_components=3).fit_predict(X_varied)
ax2.scatter(X_varied[:, 0], X_varied[:, 1], c=y_pred)
ax2.set_title("تباين غير متساوٍ")

plt.suptitle("تجميعات خليط غاوسي").set_y(0.95)
plt.show()

تجميعات خليط غاوسي, كتل موزعة بشكل غير متساوٍ, تباين غير متساوٍ

ملاحظات ختامية#

في المساحات ذات الأبعاد العالية، تميل المسافات الإقليدية إلى أن تصبح منتفخة (غير موضحة في هذا المثال). تشغيل خوارزمية تقليل الأبعاد قبل تجميع كاي-مينز يمكن أن يخفف من هذه المشكلة ويسرع الحسابات (راجع المثال تجميع مستندات النص باستخدام k-means).

في الحالة التي تكون فيها التجميعات معروفة بأنها متساوية، ولها تباين متشابه، وليست نادرة جدًا، تكون خوارزمية كاي-مينز فعالة للغاية وهي واحدة من أسرع خوارزميات التجميع المتاحة. تضيع هذه الميزة إذا كان يجب إعادة تشغيلها عدة مرات لتجنب التقارب إلى الحد الأدنى المحلي.

Total running time of the script: (0 minutes 1.390 seconds)