ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

الدالة اللوغستية#

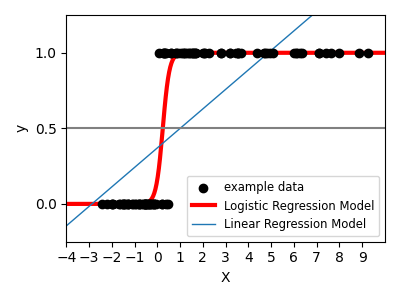
يوضح الرسم البياني كيف أن الانحدار اللوجستي، في مجموعة البيانات الاصطناعية هذه، سيصنف القيم إما 0 أو 1، أي الفئة الأولى أو الثانية، باستخدام المنحنى اللوغستي.

# المؤلفون: مطوري سكايلرن
# معرف الترخيص: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np
from scipy.special import expit

from sklearn.linear_model import LinearRegression, LogisticRegression

# توليد مجموعة بيانات تجريبية، هي عبارة عن خط مستقيم مع بعض الضوضاء الغاوسية:
xmin, xmax = -5, 5
n_samples = 100
np.random.seed(0)
X = np.random.normal(size=n_samples)
y = (X > 0).astype(float)
X[X > 0] *= 4
X += 0.3 * np.random.normal(size=n_samples)

X = X[:, np.newaxis]

# تدريب المصنف
clf = LogisticRegression(C=1e5)
clf.fit(X, y)

# رسم النتيجة
plt.figure(1, figsize=(4, 3))
plt.clf()
plt.scatter(X.ravel(), y, label="example data", color="black", zorder=20)
X_test = np.linspace(-5, 10, 300)

loss = expit(X_test * clf.coef_ + clf.intercept_).ravel()
plt.plot(X_test, loss, label="Logistic Regression Model", color="red", linewidth=3)

ols = LinearRegression()
ols.fit(X, y)
plt.plot(
    X_test,
    ols.coef_ * X_test + ols.intercept_,
    label="Linear Regression Model",
    linewidth=1,
)
plt.axhline(0.5, color=".5")

plt.ylabel("y")
plt.xlabel("X")
plt.xticks(range(-5, 10))
plt.yticks([0, 0.5, 1])
plt.ylim(-0.25, 1.25)
plt.xlim(-4, 10)
plt.legend(
    loc="lower right",
    fontsize="small",
)
plt.tight_layout()
plt.show()