ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

الانحدار باستخدام المكونات الرئيسية مقابل الانحدار باستخدام المربعات الجزئية#

يقارن هذا المثال بين Principal Component Regression (PCR) و Partial Least Squares Regression (PLS) على مجموعة بيانات تجريبية. هدفنا هو توضيح كيف يمكن لـ PLS أن يتفوق على PCR عندما يكون الهدف مرتبطًا بقوة ببعض الاتجاهات في البيانات التي لها تباين منخفض.

PCR هو منظم يتكون من خطوتين: أولاً، يتم تطبيق PCA على بيانات التدريب، مما يؤدي ربما إلى تقليل الأبعاد؛ بعد ذلك، يتم تدريب منظم (على سبيل المثال، منظم خطي) على العينات المحولة. في PCA، يكون التحول غير خاضع للإشراف تمامًا، مما يعني أنه لا يتم استخدام أي معلومات حول الأهداف. ونتيجة لذلك، قد يؤدي PCR بشكل سيء في بعض مجموعات البيانات حيث يكون الهدف مرتبطًا بقوة بـ الاتجاهات التي لها تباين منخفض. في الواقع، يؤدي تقليل الأبعاد لـ PCA إلى إسقاط البيانات في مساحة ذات أبعاد أقل حيث يتم تعظيم تباين البيانات المسقطة بشكل جشع على طول كل محور. على الرغم من أن لديهم أكبر قدرة تنبؤية على الهدف، سيتم إسقاط الاتجاهات ذات التباين المنخفض، ولن يتمكن المنظم النهائي من الاستفادة منها.

PLS هو محول ومنظم، وهو مشابه جدًا لـ PCR: فهو أيضًا يطبق تقليل الأبعاد على العينات قبل تطبيق منظم خطي على البيانات المحولة. الاختلاف الرئيسي مع PCR هو أن تحويل PLS خاضع للإشراف. لذلك، كما سنرى في هذا المثال، فإنه لا يعاني من المشكلة التي ذكرناها للتو.

# المؤلفون: مطوري scikit-learn
# معرف SPDX-License: BSD-3-Clause

البيانات#

نبدأ بإنشاء مجموعة بيانات بسيطة بميزتين. قبل أن نغوص في PCR و PLS، نقوم بتناسب مقدر PCA لعرض المكونين الرئيسيين لهذه المجموعة من البيانات، أي الاتجاهين اللذين يفسرهما معظم التباين في البيانات.

from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.cross_decomposition import PLSRegression
import matplotlib.pyplot as plt
import numpy as np

from sklearn.decomposition import PCA

rng = np.random.RandomState(0)
n_samples = 500
cov = [[3, 3], [3, 4]]
X = rng.multivariate_normal(mean=[0, 0], cov=cov, size=n_samples)
pca = PCA(n_components=2).fit(X)


plt.scatter(X[:, 0], X[:, 1], alpha=0.3, label="samples")
for i, (comp, var) in enumerate(zip(pca.components_, pca.explained_variance_)):
    comp = comp * var  # scale component by its variance explanation power
    plt.plot(
        [0, comp[0]],
        [0, comp[1]],
        label=f"Component {i}",
        linewidth=5,
        color=f"C{i + 2}",
    )
plt.gca().set(
    aspect="equal",
    title="2-dimensional dataset with principal components",
    xlabel="first feature",
    ylabel="second feature",
)
plt.legend()
plt.show()

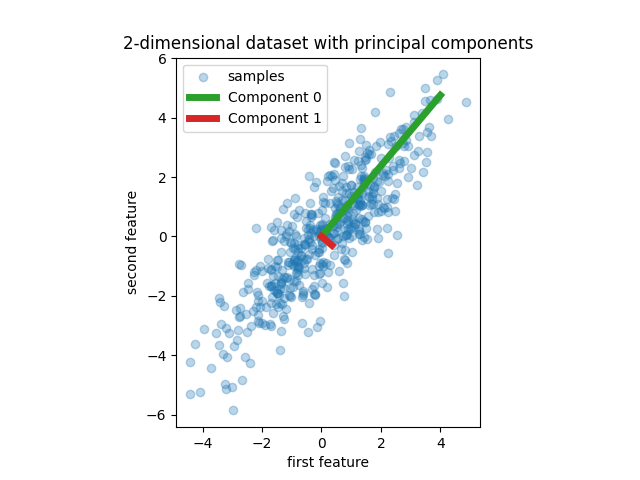
2-dimensional dataset with principal components

لغرض هذا المثال، نقوم الآن بتعريف الهدف y بحيث يكون مرتبطًا بقوة باتجاه له تباين صغير. لتحقيق هذه الغاية، سنقوم بإسقاط X على المكون الثاني، وإضافة بعض الضوضاء إليه.

y = X.dot(pca.components_[1]) + rng.normal(size=n_samples) / 2

fig, axes = plt.subplots(1, 2, figsize=(10, 3))

axes[0].scatter(X.dot(pca.components_[0]), y, alpha=0.3)
axes[0].set(xlabel="Projected data onto first PCA component", ylabel="y")
axes[1].scatter(X.dot(pca.components_[1]), y, alpha=0.3)
axes[1].set(xlabel="Projected data onto second PCA component", ylabel="y")
plt.tight_layout()
plt.show()

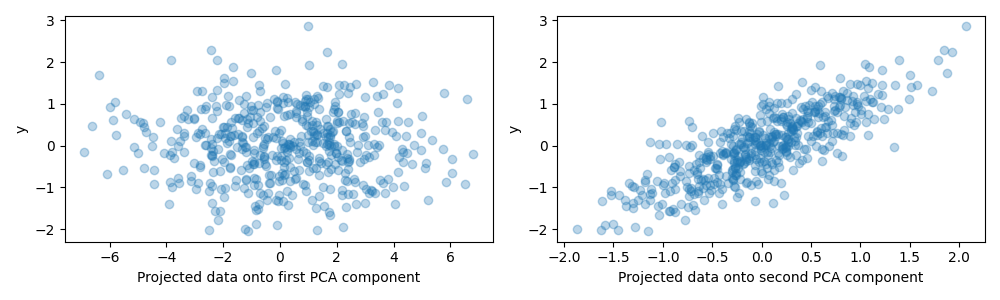
الإسقاط على مكون واحد والقدرة التنبؤية#

ننشئ الآن منظمين: PCR و PLS، ولأغراض التوضيح نقوم بتعيين عدد المكونات إلى 1. قبل تغذية البيانات إلى خطوة PCA من PCR، نقوم أولاً بتوحيدها، كما توصي الممارسة الجيدة. يحتوي مقدر PLS على قدرات قياس مدمجة.

بالنسبة لكلا النموذجين، نرسم البيانات المسقطة على المكون الأول مقابل الهدف. في كلتا الحالتين، هذه البيانات المسقطة هي ما ستستخدمه المنظمات كبيانات تدريب.

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=rng)

pcr = make_pipeline(StandardScaler(), PCA(n_components=1), LinearRegression())
pcr.fit(X_train, y_train)
pca = pcr.named_steps["pca"]  # retrieve the PCA step of the pipeline

pls = PLSRegression(n_components=1)
pls.fit(X_train, y_train)

fig, axes = plt.subplots(1, 2, figsize=(10, 3))
axes[0].scatter(pca.transform(X_test), y_test, alpha=0.3, label="ground truth")
axes[0].scatter(
    pca.transform(X_test), pcr.predict(X_test), alpha=0.3, label="predictions"
)
axes[0].set(
    xlabel="Projected data onto first PCA component", ylabel="y", title="PCR / PCA"
)
axes[0].legend()
axes[1].scatter(pls.transform(X_test), y_test, alpha=0.3, label="ground truth")
axes[1].scatter(
    pls.transform(X_test), pls.predict(X_test), alpha=0.3, label="predictions"
)
axes[1].set(xlabel="Projected data onto first PLS component",
            ylabel="y", title="PLS")
axes[1].legend()
plt.tight_layout()
plt.show()

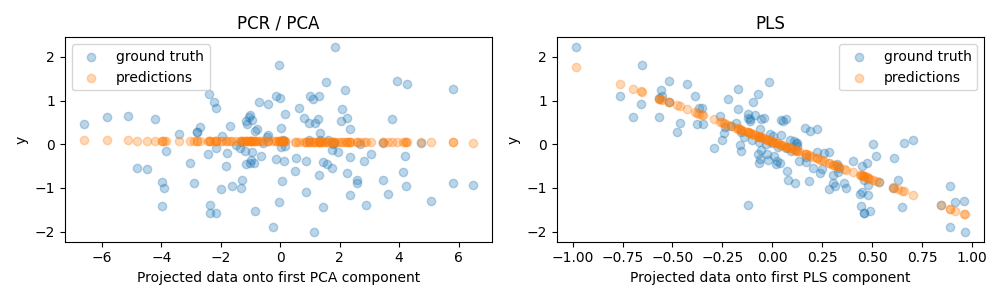
كما هو متوقع، أسقط تحويل PCA غير الخاضع للإشراف لـ PCR المكون الثاني، أي الاتجاه ذو التباين الأدنى، على الرغم من كونه الاتجاه الأكثر تنبؤًا. ويرجع ذلك إلى أن تحويل PCA غير خاضع للإشراف تمامًا، وينتج عنه بيانات مسقطة ذات قدرة تنبؤية منخفضة على الهدف.

من ناحية أخرى، يتمكن المنظم PLS من التقاط تأثير الاتجاه ذو التباين الأدنى، بفضل استخدامه لمعلومات الهدف أثناء التحول: يمكنه التعرف على أن هذا الاتجاه هو الأكثر تنبؤًا. نلاحظ أن المكون الأول لـ PLS له علاقة سلبية بالهدف، وهو ما يأتي من حقيقة أن إشارات المتجهات الذاتية تعسفية.

نطبع أيضًا درجات R-squared لكلا المقدرين، مما يؤكد أن PLS هو بديل أفضل من PCR في هذه الحالة. يشير R-squared السلبي إلى أن PCR يؤدي بشكل أسوأ من منظم سيقوم ببساطة بالتنبؤ بمتوسط الهدف.

print(f"PCR r-squared {pcr.score(X_test, y_test):.3f}")
print(f"PLS r-squared {pls.score(X_test, y_test):.3f}")

PCR r-squared -0.026
PLS r-squared 0.658

كملاحظة أخيرة، نلاحظ أن PCR بمكونين يؤدي بنفس جودة PLS: ويرجع ذلك إلى أن PCR تمكن من الاستفادة من المكون الثاني الذي له أكبر قدرة تنبؤية على الهدف.

pca_2 = make_pipeline(PCA(n_components=2), LinearRegression())
pca_2.fit(X_train, y_train)
print(f"PCR r-squared with 2 components {pca_2.score(X_test, y_test):.3f}")