ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

فشل التعلم الآلي في استنتاج الآثار السببية#

تُعد نماذج التعلم الآلي رائعة لقياس الارتباطات الإحصائية. لسوء الحظ، ما لم نكن على استعداد لوضع افتراضات قوية حول البيانات، فإن هذه النماذج غير قادرة على استنتاج الآثار السببية.

لتوضيح ذلك، سنحاكي موقفًا نحاول فيه الإجابة على أحد أهم الأسئلة في اقتصاديات التعليم: ما هو التأثير السببي للحصول على درجة جامعية على الأجور بالساعة؟ على الرغم من أن الإجابة على هذا السؤال بالغة الأهمية لواضعي السياسات، فإن الانحيازات المتغيرة المحذوفة (OVB) تمنعنا من تحديد هذا التأثير السببي.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

مجموعة البيانات: أجور بالساعة محاكاة#

يتم وضع عملية توليد البيانات في الكود أدناه. يتم استخلاص الخبرة العملية بالسنوات ومقياس القدرة من التوزيعات العادية. يتم استخلاص الأجر بالساعة لأحد الوالدين من توزيع بيتا. ثم نقوم بإنشاء مؤشر لدرجة جامعية تتأثر إيجابيًا بالقدرة والأجر بالساعة للوالدين. أخيرًا، نقوم بنمذجة الأجور بالساعة كدالة خطية لجميع المتغيرات السابقة ومكون عشوائي. لاحظ أن جميع المتغيرات لها تأثير إيجابي على الأجور بالساعة.

import numpy as np
import pandas as pd

n_samples = 10_000
rng = np.random.RandomState(32)

experiences = rng.normal(20, 10, size=n_samples).astype(int)
experiences[experiences < 0] = 0
abilities = rng.normal(0, 0.15, size=n_samples)
parent_hourly_wages = 50 * rng.beta(2, 8, size=n_samples)
parent_hourly_wages[parent_hourly_wages < 0] = 0
college_degrees = (
    9 * abilities + 0.02 * parent_hourly_wages + rng.randn(n_samples) > 0.7
).astype(int)

true_coef = pd.Series(
    {
        "college degree": 2.0,
        "ability": 5.0,
        "experience": 0.2,
        "parent hourly wage": 1.0,
    }
)
hourly_wages = (
    true_coef["experience"] * experiences
    + true_coef["parent hourly wage"] * parent_hourly_wages
    + true_coef["college degree"] * college_degrees
    + true_coef["ability"] * abilities
    + rng.normal(0, 1, size=n_samples)
)

hourly_wages[hourly_wages < 0] = 0

وصف البيانات المحاكاة#

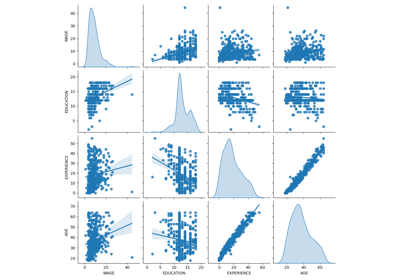
يوضح الرسم التالي توزيع كل متغير، ومخططات التشتت الزوجية. مفتاح قصة OVB الخاصة بنا هو العلاقة الإيجابية بين القدرة والدرجة الجامعية.

import seaborn as sns

df = pd.DataFrame(
    {
        "college degree": college_degrees,
        "ability": abilities,
        "hourly wage": hourly_wages,
        "experience": experiences,
        "parent hourly wage": parent_hourly_wages,
    }
)

grid = sns.pairplot(df, diag_kind="kde", corner=True)

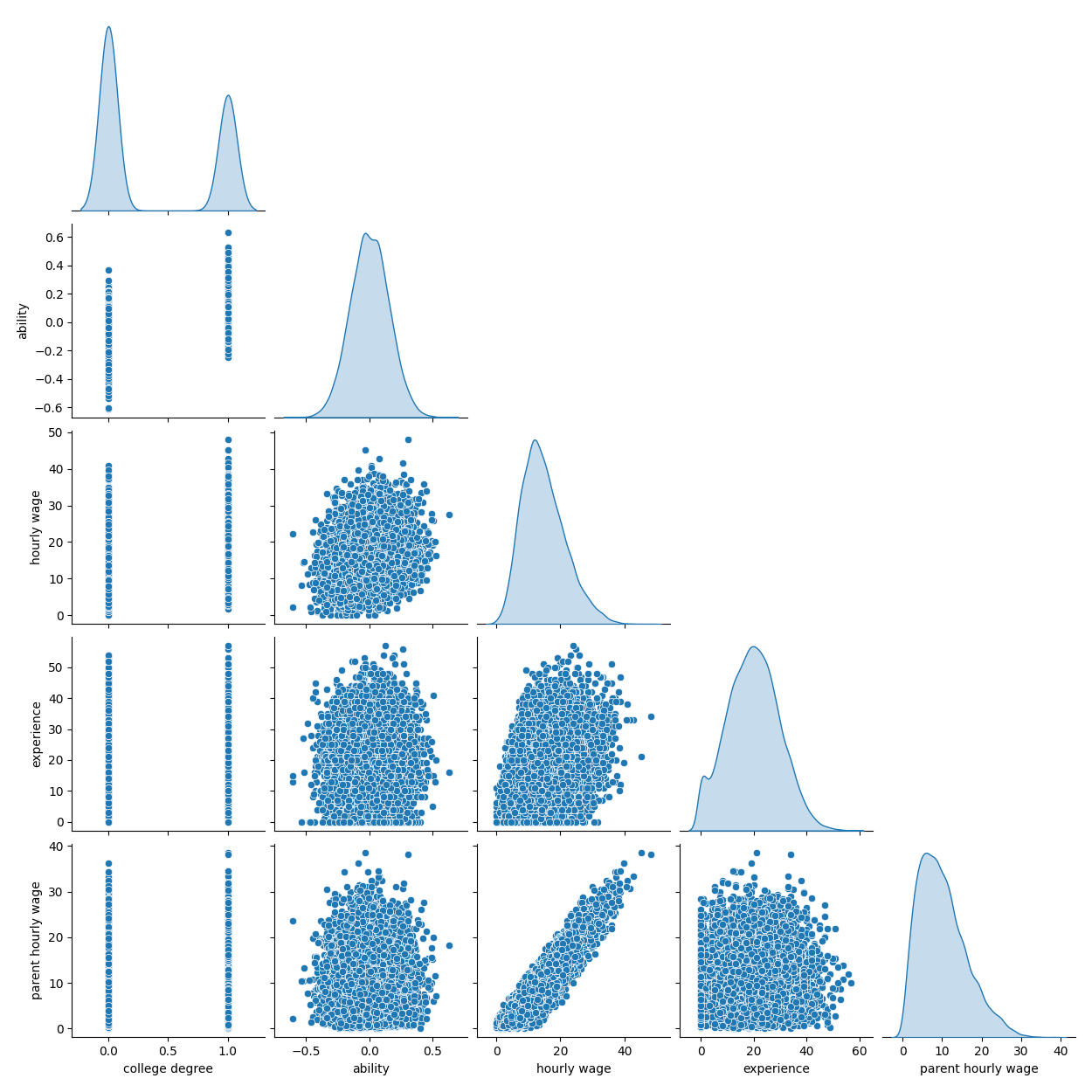
في القسم التالي، نقوم بتدريب نماذج تنبؤية، وبالتالي نقوم بتقسيم عمود الهدف من الميزات ونقسم البيانات إلى مجموعة تدريب ومجموعة اختبار.

from sklearn.model_selection import train_test_split

target_name = "hourly wage"
X, y = df.drop(columns=target_name), df[target_name]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

التنبؤ بالدخل مع المتغيرات المرصودة بالكامل#

أولاً، نقوم بتدريب نموذج تنبؤي، وهو نموذج LinearRegression. في هذه التجربة، نفترض أن جميع المتغيرات التي يستخدمها نموذج التوليد الحقيقي متاحة.

from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score

features_names = ["experience", "parent hourly wage", "college degree", "ability"]

regressor_with_ability = LinearRegression()
regressor_with_ability.fit(X_train[features_names], y_train)
y_pred_with_ability = regressor_with_ability.predict(X_test[features_names])
R2_with_ability = r2_score(y_test, y_pred_with_ability)

print(f"درجة R2 مع القدرة: {R2_with_ability:.3f}")

درجة R2 مع القدرة: 0.975

يتنبأ هذا النموذج جيدًا بالأجور بالساعة كما هو موضح بدرجة R2 العالية. نرسم معاملات النموذج لإظهار أننا نسترجع بالضبط قيم نموذج التوليد الحقيقي.

import matplotlib.pyplot as plt

model_coef = pd.Series(regressor_with_ability.coef_, index=features_names)
coef = pd.concat(
    [true_coef[features_names], model_coef],
    keys=["معاملات نموذج التوليد الحقيقي", "معاملات النموذج"],
    axis=1,
)
ax = coef.plot.barh()
ax.set_xlabel("قيم المعاملات")
ax.set_title("معاملات الانحدار الخطي بما في ذلك ميزات القدرة")
_ = plt.tight_layout()

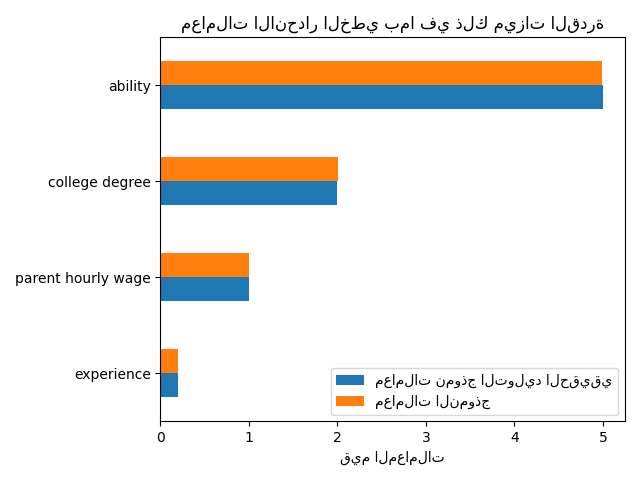
معاملات الانحدار الخطي بما في ذلك ميزات القدرة

التنبؤ بالدخل مع الملاحظات الجزئية#

من الناحية العملية، لا تتم ملاحظة القدرات الفكرية أو يتم تقديرها فقط من الوكلاء الذين يقيسون التعليم عن غير قصد أيضًا (على سبيل المثال، عن طريق اختبارات الذكاء). لكن حذف ميزة "القدرة" من نموذج خطي يؤدي إلى تضخيم التقدير من خلال OVB إيجابي.

features_names = ["experience", "parent hourly wage", "college degree"]

regressor_without_ability = LinearRegression()
regressor_without_ability.fit(X_train[features_names], y_train)
y_pred_without_ability = regressor_without_ability.predict(X_test[features_names])
R2_without_ability = r2_score(y_test, y_pred_without_ability)

print(f"درجة R2 بدون القدرة: {R2_without_ability:.3f}")

درجة R2 بدون القدرة: 0.968

القدرة التنبؤية لنموذجنا متشابهة عندما نحذف ميزة القدرة من حيث درجة R2. نتحقق الآن مما إذا كان معامل النموذج مختلفًا عن نموذج التوليد الحقيقي.

model_coef = pd.Series(regressor_without_ability.coef_, index=features_names)
coef = pd.concat(
    [true_coef[features_names], model_coef],
    keys=["معاملات نموذج التوليد الحقيقي", "معاملات النموذج"],
    axis=1,
)
ax = coef.plot.barh()
ax.set_xlabel("قيم المعاملات")
_ = ax.set_title("معاملات الانحدار الخطي باستثناء ميزة القدرة")
plt.tight_layout()
plt.show()

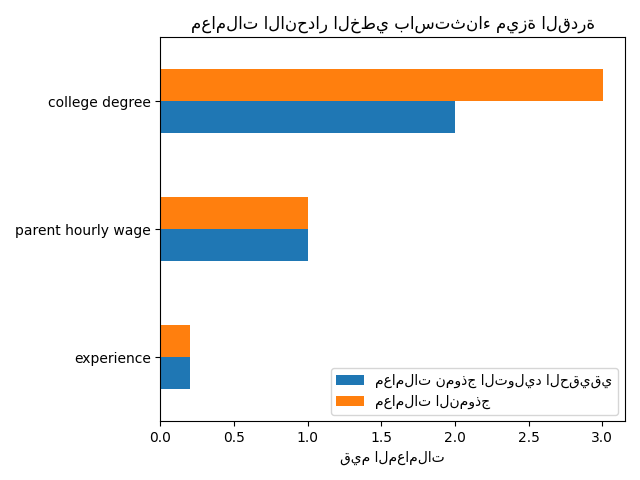
معاملات الانحدار الخطي باستثناء ميزة القدرة

للتعويض عن المتغير المحذوف، يقوم النموذج بتضخيم معامل ميزة الدرجة الجامعية. لذلك، فإن تفسير قيمة هذا المعامل كتأثير سببي لنموذج التوليد الحقيقي غير صحيح.

الدروس المستفادة#

لم يتم تصميم نماذج التعلم الآلي لتقدير الآثار السببية. بينما أظهرنا ذلك بنموذج خطي، يمكن أن يؤثر OVB على أي نوع من النماذج.

عند تفسير معامل أو تغيير في التنبؤات ناتج عن تغيير في إحدى الميزات، من المهم أن تضع في اعتبارك المتغيرات التي يحتمل ألا تتم ملاحظتها والتي يمكن أن تكون مرتبطة بكل من الميزة المعنية والمتغير الهدف. تسمى هذه المتغيرات المتغيرات المربكة. من أجل تقدير التأثير السببي في وجود التشويش، عادةً ما يجري الباحثون تجارب يتم فيها اختيار متغير المعالجة (مثل الدرجة الجامعية) عشوائيًا. عندما تكون التجربة باهظة الثمن أو غير أخلاقية، يمكن للباحثين أحيانًا استخدام تقنيات استدلال سببي أخرى مثل تقديرات المتغيرات الآلية (IV).

Total running time of the script: (0 minutes 3.267 seconds)