ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
العمليات الغاوسية على هياكل البيانات المنقوصة#
يوضح هذا المثال استخدام العمليات الغاوسية لمهام الانحدار والتصنيف على البيانات التي ليست في شكل متجه ميزات بطول ثابت. يتم تحقيق ذلك من خلال استخدام دوال النواة التي تعمل مباشرة على هياكل منقوصة مثل التسلسلات متغيرة الطول والأشجار والرسوم البيانية.
على وجه التحديد، هنا المتغيرات المدخلة هي بعض تسلسلات الجينات المخزنة كسلاسل متغيرة الطول تتكون من الأحرف 'A' و 'T' و 'C' و 'G'، بينما المتغيرات المخرجة هي أرقام فاصلة عائمة وتسميات صحيح/خطأ في مهام الانحدار والتصنيف، على التوالي.
يتم تعريف نواة بين تسلسلات الجينات باستخدام الالتفاف R [1] عن طريق دمج نواة ثنائية حرفية على جميع أزواج الأحرف بين زوج من السلاسل.
سيولد هذا المثال ثلاثة أشكال.
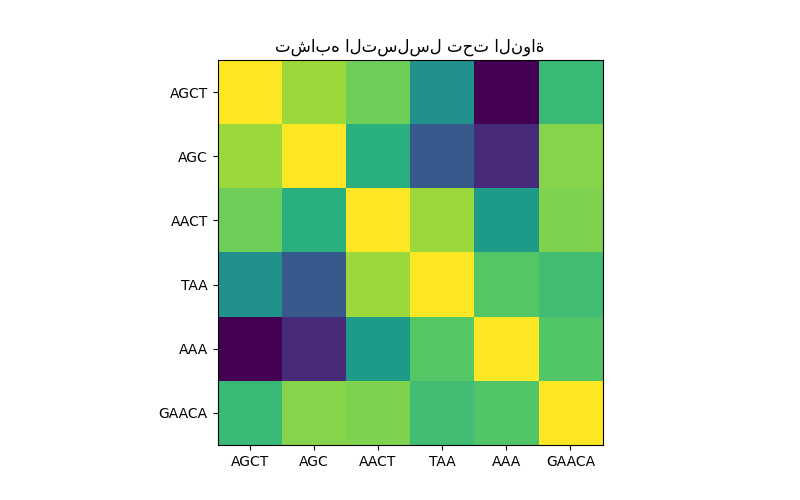
في الشكل الأول، نقوم بتصور قيمة النواة، أي تشابه التسلسلات، باستخدام خريطة ألوان. يشير اللون الأكثر سطوعًا هنا إلى تشابه أعلى.
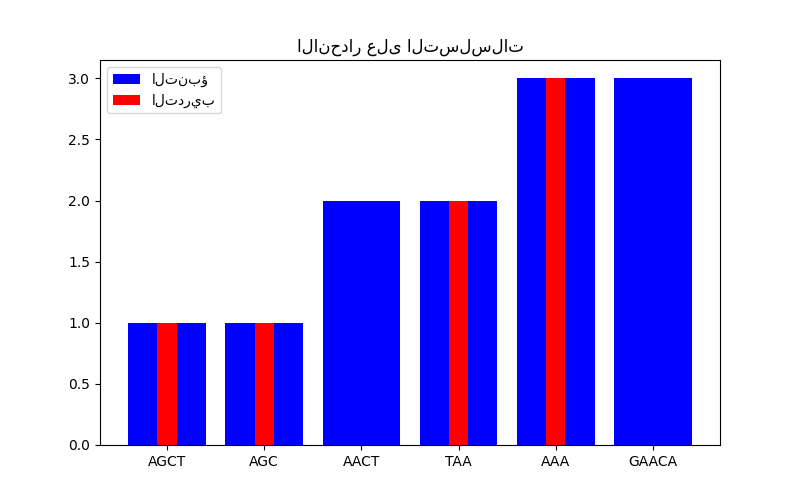
في الشكل الثاني، نعرض بعض نتائج الانحدار على مجموعة بيانات من 6 تسلسلات. هنا نستخدم التسلسلات الأول والثاني والرابع والخامس كمجموعة تدريب لإجراء تنبؤات على التسلسلين الثالث والسادس.
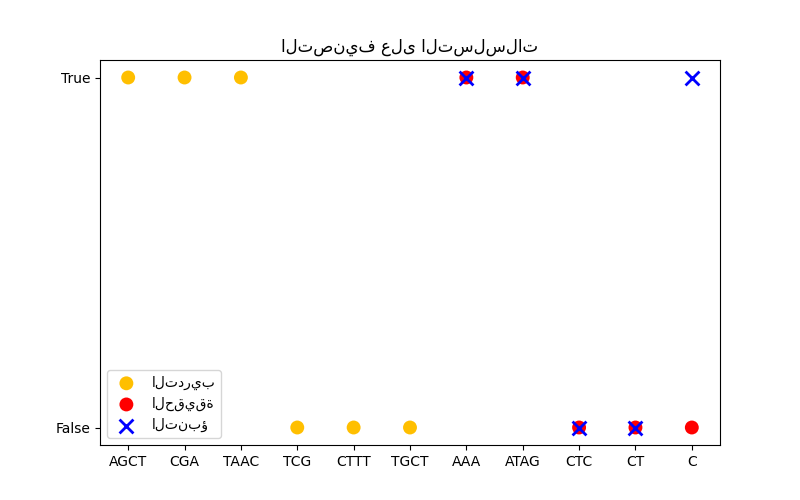
في الشكل الثالث، نوضح نموذج تصنيف عن طريق التدريب على 6 تسلسلات وإجراء تنبؤات على 5 تسلسلات أخرى. الحقيقة الأساسية هنا هي ببساطة ما إذا كان هناك حرف 'A' واحد على الأقل في التسلسل. هنا يقوم النموذج بأربعة تصنيفات صحيحة ويفشل في واحد.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import numpy as np
from sklearn.base import clone
from sklearn.gaussian_process import GaussianProcessClassifier, GaussianProcessRegressor
from sklearn.gaussian_process.kernels import GenericKernelMixin, Hyperparameter, Kernel
class SequenceKernel(GenericKernelMixin, Kernel):
"""
نواة التواء بسيطة (لكنها صالحة) لتسلسلات ذات أطوال متغيرة.
"""
def __init__(self, baseline_similarity=0.5, baseline_similarity_bounds=(1e-5, 1)):
self.baseline_similarity = baseline_similarity
self.baseline_similarity_bounds = baseline_similarity_bounds
@property
def hyperparameter_baseline_similarity(self):
return Hyperparameter(
"baseline_similarity", "numeric", self.baseline_similarity_bounds
)
def _f(self, s1, s2):
"""
قيمة النواة بين زوج من التسلسلات
"""
return sum(
[1.0 if c1 == c2 else self.baseline_similarity for c1 in s1 for c2 in s2]
)
def _g(self, s1, s2):
"""
مشتق النواة بين زوج من التسلسلات
"""
return sum([0.0 if c1 == c2 else 1.0 for c1 in s1 for c2 in s2])
def __call__(self, X, Y=None, eval_gradient=False):
if Y is None:
Y = X
if eval_gradient:
return (
np.array([[self._f(x, y) for y in Y] for x in X]),
np.array([[[self._g(x, y)] for y in Y] for x in X]),
)
else:
return np.array([[self._f(x, y) for y in Y] for x in X])
def diag(self, X):
return np.array([self._f(x, x) for x in X])
def is_stationary(self):
return False
def clone_with_theta(self, theta):
cloned = clone(self)
cloned.theta = theta
return cloned
kernel = SequenceKernel()
مصفوفة تشابه التسلسل تحت النواة#
import matplotlib.pyplot as plt
X = np.array(["AGCT", "AGC", "AACT", "TAA", "AAA", "GAACA"])
K = kernel(X)
D = kernel.diag(X)
plt.figure(figsize=(8, 5))
plt.imshow(np.diag(D**-0.5).dot(K).dot(np.diag(D**-0.5)))
plt.xticks(np.arange(len(X)), X)
plt.yticks(np.arange(len(X)), X)
plt.title("تشابه التسلسل تحت النواة")
plt.show()
الانحدار#
X = np.array(["AGCT", "AGC", "AACT", "TAA", "AAA", "GAACA"])
Y = np.array([1.0, 1.0, 2.0, 2.0, 3.0, 3.0])
training_idx = [0, 1, 3, 4]
gp = GaussianProcessRegressor(kernel=kernel)
gp.fit(X[training_idx], Y[training_idx])
plt.figure(figsize=(8, 5))
plt.bar(np.arange(len(X)), gp.predict(X), color="b", label="التنبؤ")
plt.bar(training_idx, Y[training_idx], width=0.2, color="r", alpha=1, label="التدريب")
plt.xticks(np.arange(len(X)), X)
plt.title("الانحدار على التسلسلات")
plt.legend()
plt.show()
التصنيف#
X_train = np.array(["AGCT", "CGA", "TAAC", "TCG", "CTTT", "TGCT"])
# ما إذا كان هناك 'A' في التسلسل
Y_train = np.array([True, True, True, False, False, False])
gp = GaussianProcessClassifier(kernel)
gp.fit(X_train, Y_train)
X_test = ["AAA", "ATAG", "CTC", "CT", "C"]
Y_test = [True, True, False, False, False]
plt.figure(figsize=(8, 5))
plt.scatter(
np.arange(len(X_train)),
[1.0 if c else -1.0 for c in Y_train],
s=100,
marker="o",
edgecolor="none",
facecolor=(1, 0.75, 0),
label="التدريب",
)
plt.scatter(
len(X_train) + np.arange(len(X_test)),
[1.0 if c else -1.0 for c in Y_test],
s=100,
marker="o",
edgecolor="none",
facecolor="r",
label="الحقيقة",
)
plt.scatter(
len(X_train) + np.arange(len(X_test)),
[1.0 if c else -1.0 for c in gp.predict(X_test)],
s=100,
marker="x",
facecolor="b",
linewidth=2,
label="التنبؤ",
)
plt.xticks(np.arange(len(X_train) + len(X_test)), np.concatenate((X_train, X_test)))
plt.yticks([-1, 1], [False, True])
plt.title("التصنيف على التسلسلات")
plt.legend()
plt.show()
/project/workspace/sklearn/gaussian_process/kernels.py:442: ConvergenceWarning:
The optimal value found for dimension 0 of parameter baseline_similarity is close to the specified lower bound 1e-05. Decreasing the bound and calling fit again may find a better value.
Total running time of the script: (0 minutes 0.257 seconds)
Related examples