Normal, Ledoit-Wolf and OAS Linear Discriminant Analysis for classification

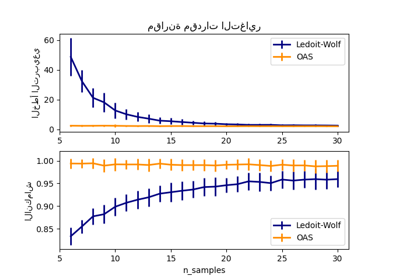
هذا المثال يوضح كيف أن مقدرات Ledoit-Wolf وOracle Approximating Shrinkage (OAS) لمصفوفة التباين يمكن أن تحسن التصنيف.

# المؤلفون: مطوري scikit-learn
# معرف الترخيص: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.covariance import OAS
from sklearn.datasets import make_blobs
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

n_train = 20  # عدد العينات للتدريب
n_test = 200  # عدد العينات للاختبار
n_averages = 50  # عدد مرات تكرار التصنيف
n_features_max = 75  # الحد الأقصى لعدد الميزات
step = 4  # حجم الخطوة للحساب


def generate_data(n_samples, n_features):
    """توليد بيانات عشوائية شبيهة بالكرات مع ميزات ضوضائية.

    هذه الدالة تعيد مصفوفة بيانات الإدخال بشكل `(n_samples, n_features)`
    ومصفوفة لعلامات التصنيف `n_samples`.

    ميزة واحدة فقط تحتوي على معلومات تمييزية، والميزات الأخرى
    تحتوي فقط على ضوضاء.
    """
    X, y = make_blobs(n_samples=n_samples, n_features=1, centers=[[-2], [2]])

    # إضافة ميزات غير تمييزية
    if n_features > 1:
        X = np.hstack([X, np.random.randn(n_samples, n_features - 1)])
    return X, y


acc_clf1, acc_clf2, acc_clf3 = [], [], []
n_features_range = range(1, n_features_max + 1, step)
for n_features in n_features_range:
    score_clf1, score_clf2, score_clf3 = 0, 0, 0
    for _ in range(n_averages):
        X, y = generate_data(n_train, n_features)

        clf1 = LinearDiscriminantAnalysis(
            solver="lsqr", shrinkage=None).fit(X, y)
        clf2 = LinearDiscriminantAnalysis(
            solver="lsqr", shrinkage="auto").fit(X, y)
        oa = OAS(store_precision=False, assume_centered=False)
        clf3 = LinearDiscriminantAnalysis(solver="lsqr", covariance_estimator=oa).fit(
            X, y
        )

        X, y = generate_data(n_test, n_features)
        score_clf1 += clf1.score(X, y)
        score_clf2 += clf2.score(X, y)
        score_clf3 += clf3.score(X, y)

    acc_clf1.append(score_clf1 / n_averages)
    acc_clf2.append(score_clf2 / n_averages)
    acc_clf3.append(score_clf3 / n_averages)

features_samples_ratio = np.array(n_features_range) / n_train

plt.plot(
    features_samples_ratio,
    acc_clf1,
    linewidth=2,
    label="LDA",
    color="gold",
    linestyle="solid",
)
plt.plot(
    features_samples_ratio,
    acc_clf2,
    linewidth=2,
    label="LDA with Ledoit Wolf",
    color="navy",
    linestyle="dashed",
)
plt.plot(
    features_samples_ratio,
    acc_clf3,
    linewidth=2,
    label="LDA with OAS",
    color="red",
    linestyle="dotted",
)

plt.xlabel("n_features / n_samples")
plt.ylabel("Classification accuracy")

plt.legend(loc="lower left")
plt.ylim((0.65, 1.0))
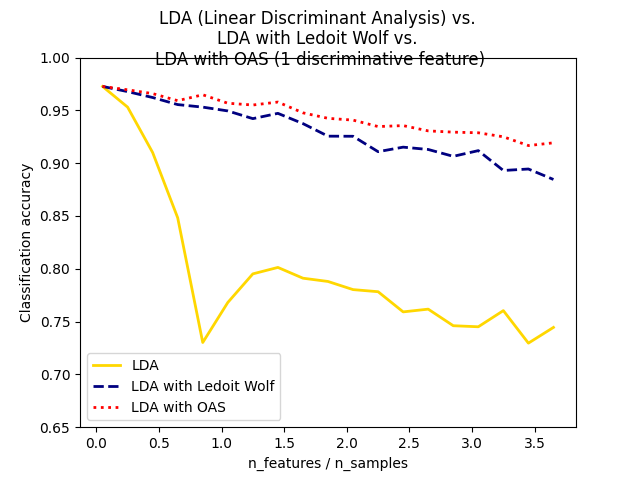
plt.suptitle(
    "LDA (Linear Discriminant Analysis) vs. "
    + "\n"
    + "LDA with Ledoit Wolf vs. "
    + "\n"
    + "LDA with OAS (1 discriminative feature)"
)
plt.show()

Related examples

تقدير Ledoit-Wolf مقابل OAS

تقدير Ledoit-Wolf مقابل OAS

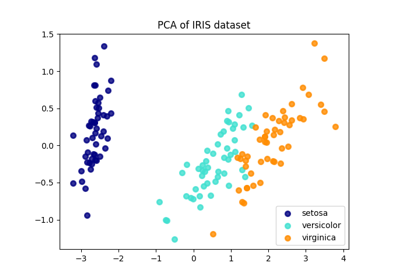
مقارنة بين الإسقاط ثنائي الأبعاد للمجموعة البيانات آيريس باستخدام LDA وPCA

مقارنة بين الإسقاط ثنائي الأبعاد للمجموعة البيانات آيريس باستخدام LDA وPCA

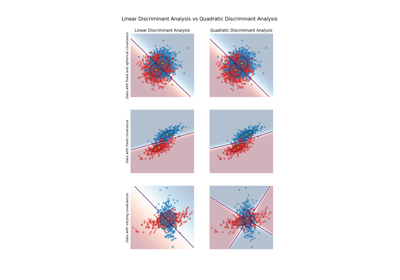
sphx_glr_auto_examples_classification_plot_lda_qda.py

هذا مثال لرسم حدود التمييز والقطع الناقص لتشتت كل فئة، والتي تم تعلمها بواسطة LinearDiscriminantAnalysis (LDA) و QuadraticDiscriminantAnalysis (QDA). يُظهر القطع الناقص الانحراف المعياري المزدوج لكل فئة. مع LDA، يكون الانحراف المعياري هو نفسه لجميع الفئات، في حين أن لكل فئة انحرافها المعياري الخاص بها مع QDA.

الحد من الأبعاد باستخدام تحليل مكونات الجوار

الحد من الأبعاد باستخدام تحليل مكونات الجوار