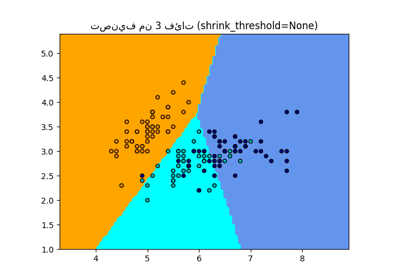
ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
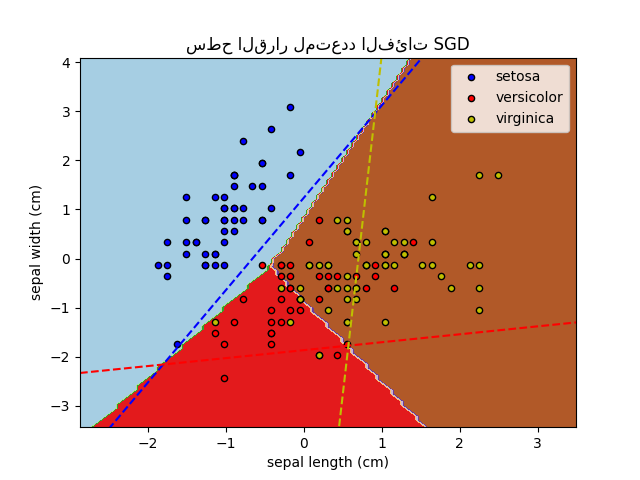
رسم متعدد الفئات SGD على مجموعة بيانات الزهرة#
رسم سطح القرار لمتعدد الفئات SGD على مجموعة بيانات الزهرة. تمثل الخطوط المتقطعة المستويات الفاصلة المقابلة للثلاثة مصنفات من نوع واحد مقابل الجميع (OVA).
# المؤلفون: مطوري مكتبة ساي كيت ليرن
# معرف رخصة SPDX: BSD-3-Clause
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.inspection import DecisionBoundaryDisplay
from sklearn.linear_model import SGDClassifier
# استيراد بعض البيانات للتجربة
iris = datasets.load_iris()
# نأخذ فقط أول ميزتين. يمكننا
# تجنب هذا التقطيع غير المناسب باستخدام مجموعة بيانات ثنائية الأبعاد
X = iris.data[:, :2]
y = iris.target
colors = "bry"
# الخلط
idx = np.arange(X.shape[0])
np.random.seed(13)
np.random.shuffle(idx)
X = X[idx]
y = y[idx]
# التوحيد
mean = X.mean(axis=0)
std = X.std(axis=0)
X = (X - mean) / std
clf = SGDClassifier(alpha=0.001, max_iter=100).fit(X, y)
ax = plt.gca()
DecisionBoundaryDisplay.from_estimator(
clf,
X,
cmap=plt.cm.Paired,
ax=ax,
response_method="predict",
xlabel=iris.feature_names[0],
ylabel=iris.feature_names[1],
)
plt.axis("tight")
# رسم نقاط التدريب أيضًا
for i, color in zip(clf.classes_, colors):
idx = np.where(y == i)
plt.scatter(
X[idx, 0],
X[idx, 1],
c=color,
label=iris.target_names[i],
edgecolor="black",
s=20,
)
plt.title("سطح القرار لمتعدد الفئات SGD")
plt.axis("tight")
# رسم المصنفات الثلاثة من نوع واحد مقابل الجميع
xmin, xmax = plt.xlim()
ymin, ymax = plt.ylim()
coef = clf.coef_
intercept = clf.intercept_
def plot_hyperplane(c, color):
def line(x0):
return (-(x0 * coef[c, 0]) - intercept[c]) / coef[c, 1]
plt.plot([xmin, xmax], [line(xmin), line(xmax)], ls="--", color=color)
for i, color in zip(clf.classes_, colors):
plot_hyperplane(i, color)
plt.legend()
plt.show()
Total running time of the script: (0 minutes 0.137 seconds)
Related examples
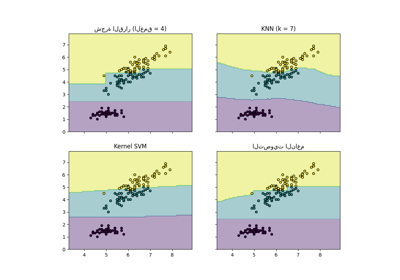
رسم سطح القرار لأشجار القرار المدربة على مجموعة بيانات الزهرة الآرغوانية
رسم سطح القرار لأشجار القرار المدربة على مجموعة بيانات الزهرة الآرغوانية
تحليل المكونات الرئيسية (PCA) على مجموعة بيانات Iris
تحليل المكونات الرئيسية (PCA) على مجموعة بيانات Iris