<no title> — scikit-learn 1.6.dev0 documentation

ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

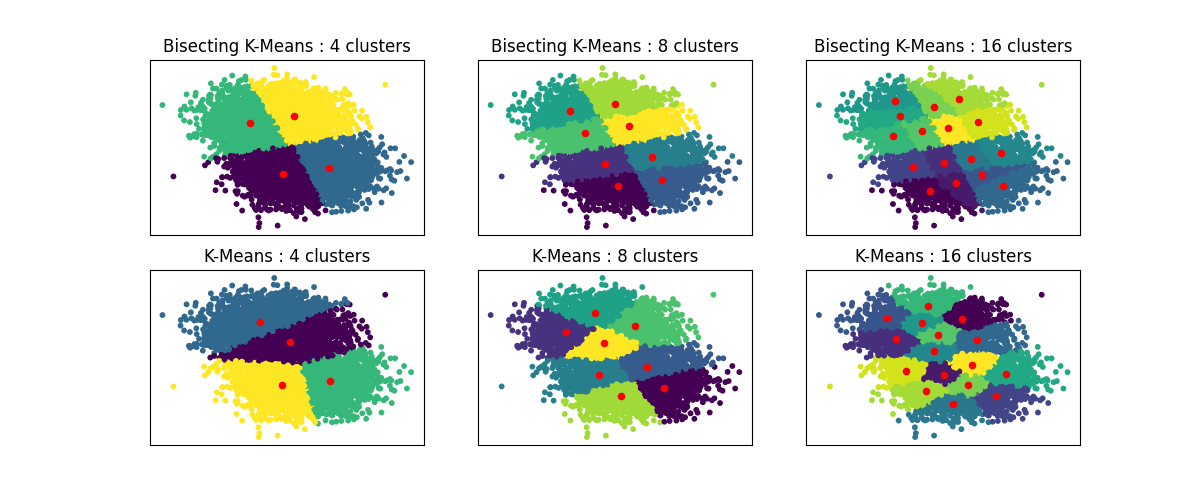
هذا المثال يوضح الفروق بين خوارزمية K-Means العادية وخوارزمية Bisecting K-Means.

في حين أن التجميعات في خوارزمية K-Means تختلف عند زيادة n_clusters، فإن تجميع Bisecting K-Means يبني على التجميعات السابقة. ونتيجة لذلك، فإنها تميل إلى إنشاء مجموعات ذات بنية واسعة النطاق أكثر انتظامًا. يمكن ملاحظة هذا الاختلاف بصريًا: بالنسبة لجميع أعداد المجموعات، هناك خط فاصل يقسم سحابة البيانات الكلية إلى نصفين في خوارزمية BisectingKMeans، وهو غير موجود في خوارزمية K-Means العادية.

Bisecting K-Means : 4 clusters, Bisecting K-Means : 8 clusters, Bisecting K-Means : 16 clusters, K-Means : 4 clusters, K-Means : 8 clusters, K-Means : 16 clusters

# المؤلفون: مطوري scikit-learn
# معرف الترخيص: BSD-3-Clause

import matplotlib.pyplot as plt

from sklearn.cluster import BisectingKMeans, KMeans
from sklearn.datasets import make_blobs

print(__doc__)


# توليد بيانات العينة
n_samples = 10000
random_state = 0

X, _ = make_blobs(n_samples=n_samples, centers=2, random_state=random_state)

# عدد مراكز التجميع لخوارزميتي KMeans و BisectingKMeans
n_clusters_list = [4, 8, 16]

# الخوارزميات المراد مقارنتها
clustering_algorithms = {
    "Bisecting K-Means": BisectingKMeans,
    "K-Means": KMeans,
}

# إنشاء مخططات فرعية لكل متغير
fig, axs = plt.subplots(
    len(clustering_algorithms), len(n_clusters_list), figsize=(12, 5)
)

axs = axs.T

for i, (algorithm_name, Algorithm) in enumerate(clustering_algorithms.items()):
    for j, n_clusters in enumerate(n_clusters_list):
        algo = Algorithm(n_clusters=n_clusters, random_state=random_state, n_init=3)
        algo.fit(X)
        centers = algo.cluster_centers_

        axs[j, i].scatter(X[:, 0], X[:, 1], s=10, c=algo.labels_)
        axs[j, i].scatter(centers[:, 0], centers[:, 1], c="r", s=20)

        axs[j, i].set_title(f"{algorithm_name} : {n_clusters} clusters")


# إخفاء تسميات المحور وتسميات التكتات للأشكال العلوية وتكتات المحور y للأشكال اليمنى.
for ax in axs.flat:
    ax.label_outer()
    ax.set_xticks([])
    ax.set_yticks([])

plt.show()